Eccfrog512ck2：一种增强型512位Weierstrass椭圆曲线

Eccfrog512ck2：一种增强的 512 位 Weierstrass 椭圆曲线

本文概述了 Víctor Duarte Melo 和我最近一直在做的研究工作。

引言

我进入密码学的道路……我首先爱上了 Diffie-Hellman 方法的力量，然后惊叹于 RSA 方法的简单性和力量。但正是在椭圆曲线密码学中，我发现了密码学的纯粹之美。对我来说，如此简单和优雅的东西怎么能带来如此强大的力量？

虽然我们进入 Diffie-Hellman 方法世界的第一步是使用离散对数（g^x mod p），但正是椭圆曲线的力量使其变得更加简单，而且现在我们几乎所有与互联网的连接都受到 ECDH（椭圆曲线 Diffie Hellman）的保护。对于数字签名，椭圆曲线也大大降低了处理要求，并且我们现在经常使用 ECDSA 和 EdDSA 而不是 RSA。

比特币和以太坊

椭圆曲线的迅速崛起可能发生在 Satoshi Nakamoto 为比特币选择了 secp256k1 曲线时。它使用以下等式：

y² = x³ + 7 (mod p)

其中 p=2²⁵⁶-2³²-977，并被定义为 Weierstrass 曲线。总的来说，我们最终得到了一些整数点 (x,y)，其中 secp256k1 的前 20 个点是 [这里]：

Elliptic curve is:  secp256k1
Finding elliptic point closest to: 1
Prime number:   115792089237316195423570985008687907853269984665640564039457584007908834671663
a,b 0 7
(1, 29896722852569046015560700294576055776214335159245303116488692907525646231534L)
(2, 69211104694897500952317515077652022726490027694212560352756646854116994689233L)
(3, 94471189679404635060807731153122836805497974241028285133722790318709222555876L)
(4, 40508090799132825824753983223610497876805216745196355809233758402754120847507L)
(6, 19112057249303445409876026535760519114630369653212530612662492210011362204224L)
(8, 91736135629086734185706894124002126994554994840140056297753929940646699135966L)
(12, 84723224514829953401809146057688111907524826729556536824205543511930558249867L)
(13, 20267456347483554069520440766283645831919514026818877192810320909941447705364L)
(14, 44647516152956573151520437476900496747965187933683819148138195218441524686495L)
(16, 6086653149631013477190265492692874244435390487330439650246572165529255539543L)
(20, 95115947350322555212584100192293494006877237570979160767752142956238074546829L)

虽然 secp256k1 用于许多区块链系统中，但我们通常使用 secp256r1 (NIST P256) 进行 TLS 通信。

对于 secp256k1，我们具有 128 位安全性，这为当前建议的 112 位安全级别提供了良好的余量。 但是，在某些应用程序中，我们需要更高的安全级别，并且必须为椭圆曲线使用更大的素数。 对于 NIST，最安全的曲线是 NIST P521，它使用的素数为 2⁵²¹−1。 它采用以下形式 [这里]：

y ²= x ³−3 x + b =1093849…5984,

以及一个有限域：

p =2⁵²¹−1=6864797….51

总的来说，我们在曲线上有一个基点 (G)，然后可以计算 2G (G+G) 和 3G (G+G+G)：

P512
Point 1G: (2661740802050217063228768716723360960729859168756973147706671368418802944996427808491545080627771902352094241225065558662157113545570916814161637315895999846, 3757180025770020463545507224491183603594455134769762486694567779615544477440556316691234405012945539562144444537289428522585666729196580810124344277578376784)
(1G) in hex: 0xc6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66,0x11839296a789a3bc0045c8a5fb42c7d1bd998f54449579b446817afbd17273e662c97ee72995ef42640c550b9013fad0761353c7086a272c24088be94769fd16650)

Point 2G: (901472452850866198617673658578940391618730359691416279093035377195377079020397774511960179466499271590922803070095487687963115616363390991670183687363590205, 3281327921582527507824747162491172657218985358085640380741461489720525905953211486053138004786012424348623853685340634287932228687534583594738661002099038978)
(2G) in hex: 0x433c219024277e7e682fcb288148c282747403279b1ccc06352c6e5505d769be97b3b204da6ef55507aa104a3a35c5af41cf2fa364d60fd967f43e3933ba6d783d,0xf4bb8cc7f86db26700a7f3eceeeed3f0b5c6b5107c4da97740ab21a29906c42dbbb3e377de9f251f6b93937fa99a3248f4eafcbe95edc0f4f71be356d661f41b02)

Point 3G: (5674708455687314755177411224894914551247560982429925442328503936381769479291831722549724502783064471579811889182869230569934709210549404604394803481732951421, 4271801692429350493774172787940824381696861087943454989753620357811953134117882851809933515614164977926164094992857584446095333607804956469237639174332793061)
(3G) in hex: 0x1a73d352443de29195dd91d6a64b5959479b52a6e5b123d9ab9e5ad7a112d7a8dd1ad3f164a3a4832051da6bd16b59fe21baeb490862c32ea05a5919d2ede37ad7d,0x13e9b03b97dfa62ddd9979f86c6cab814f2f1557fa82a9d0317d2f8ab1fa355ceec2e2dd4cf8dc575b02d5aced1dec3c70cf105c9bc93a590425f588ca1ee86c0e5)

Eccfrog512ck2：增强的 512 位 Weierstrass 椭圆曲线

通过与 Víctor Duarte Melo 合作，我们开发了一种增强的椭圆曲线，该曲线提高了 P521 的性能，并命名为 eccfrog512ck2。 它已在 IACR [这里] 中发布：

曲线的基本规范是：

我们可以看到它对扭曲和 MOV 攻击具有抵抗力。 选择的参数是：

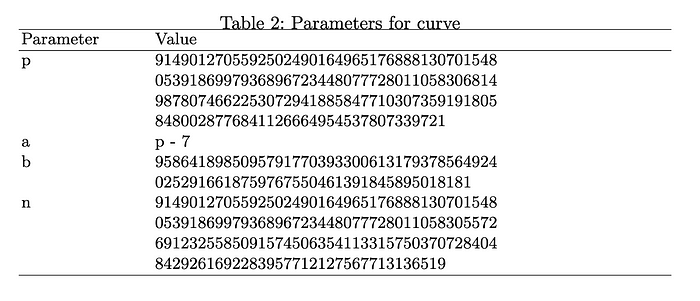
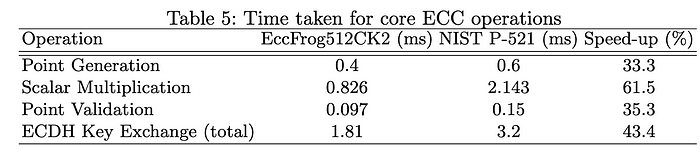
其中 n 是曲线的阶数——它定义了可能的 (x,y) 点的数量。 在性能方面，在我们的评估中，我们获得了基本椭圆曲线运算的显着改进，例如点生成、标量乘法 (k.G)、点验证（点是否在曲线上）和 ECDH 密钥交换时间：

结论

这是论文：

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～