基于Rabin方法的可证明安全公钥加密

使用 Rabin 方法的可证明安全公钥加密

嗯，RSA 公钥加密方法已经有近 50 年的历史了，但它仍然没有对其安全性的正式证明。多年来，它做得很好，并且通常设法提高其计算难度，以跟上计算能力的进步。虽然人们认为 RSA 的难度是基于将模数 (n) 分解为其素数因子，但它不是一种可证明安全的方法，而且明天，有人可能会找到绕过基本方法的方法。然而，第一个证明其安全性的公钥加密方法是 Rabin 公钥加密方法 [1]。这是由强大的 Michael O Rabin 创建的 [here]。

注意: 显然，难题是整数分解，而离散对数在量子破解方面是不安全的，但是，目前，它们在计算上是困难的。

Rabin 公钥

使用 Rabin 公钥，我们选择两个素数（p 和 q）。如果可能的话，p ≡ q ≡3 (mod 4) 可以简化解密过程。最初，我们确定：

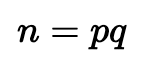
是公钥，而 p 和 q 是私钥。我们用 n 加密，用 n 的因子 p 和 q 解密。要加密，让明文为 P ={0,…, n −1}，消息 m ∈ P。然后密文（c）是：

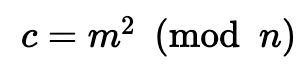
然后解密是：

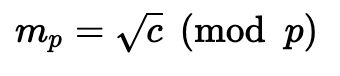
和

有关解密过程的更多详细信息 [here]。

示例

让我们取两个素数 p=7 和 q=11。那么 n 将等于 77，并给出 {1, 2 … 76} 的明文空间 (P)。如果我们有一条消息 (m=5)，那么密码将是 c =5² (mod 77)，即 25。我们现在可以运行一个小的 Python 程序来查看每个可能的消息 ( c = m² (mod n))有多少相同的密码：

p=7
q=11

n=p*q
m = 5
find=m**2 % n,
for i in range(1,n-1):
    c=i**2 % n,
    if (find==c): print "(%d->%s*)" % (i,c[0]),
    else: print "(%d-> %s)" % (i,c[0]),

此输出显示了密码消息 m=5 的匹配项：

(1-> 1) (2-> 4) (3-> 9) (4-> 16) (5->25*) (6-> 36) (7-> 49) (8-> 64)
(9-> 4) (10-> 23) (11-> 44) (12-> 67) (13-> 15) (14-> 42) (15-> 71)
(16->25*) (17-> 58) (18-> 16) (19-> 53) (20-> 15) (21-> 56) (22-> 22)
(23-> 67) (24-> 37) (25-> 9) (26-> 60) (27-> 36) (28-> 14) (29-> 71)
(30-> 53) (31-> 37) (32-> 23) (33-> 11) (34-> 1) (35-> 70) (36-> 64)
(37-> 60) (38-> 58) (39-> 58) (40-> 60) (41-> 64) (42-> 70) (43-> 1)
(44-> 11) (45-> 23) (46-> 37) (47-> 53) (48-> 71) (49-> 14) (50-> 36)
(51-> 60) (52-> 9) (53-> 37) (54-> 67) (55-> 22) (56-> 56) (57-> 15)
(58-> 53) (59-> 16) (60-> 58) (61->25*) (62-> 71) (63-> 42) (64-> 15)
(65-> 67) (66-> 44) (67-> 23) (68-> 4) (69-> 64) (70-> 49) (71-> 36)
(72->25*) (73-> 16) (74-> 9) (75-> 4)

我们可以看到，我们得到了与 m=5 相同的四个可能的密码结果。它们是 (m=5,c=25)、(m=16,c=25)、(m=61,c=25) 和 (m=72,c=25)。情况总是这样，因此挑战是找到正确映射回消息的那个。因此，Rabin 密码系统被称为四合一方法。

要解密，我们使用中国剩余定理，使用 √c(mod p) 和 √c(mod) 运算。如果我们选择素数 p ≡ q ≡3(mod4)，则解密很简单：

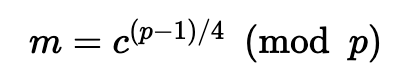
编码

编码（基于 [ code]）在此 [here]:

import random
from Crypto.Util.number import *
import codecs
import Crypto
from Crypto import Random

def encryption(plaintext, n):
    # c = m^2 mod n
    plaintext = padding(plaintext)
    return plaintext ** 2 % n

def padding(plaintext):
    binary_str = bin(plaintext)     # convert to a bit string # 转换为位字符串
    output = binary_str + binary_str[-16:]      # pad the last 16 bits to the end # 将最后 16 位填充到末尾
    return int(output, 2)       # convert back to integer # 转换回整数
def decryption(a, p, q):
    n = p * q
    r, s = 0, 0
    # find sqrt # 查找平方根
    # for p # 对于 p
    if p % 4 == 3:
        r = sqrt_p_3_mod_4(a, p)
    elif p % 8 == 5:
        r = sqrt_p_5_mod_8(a, p)
    # for q # 对于 q
    if q % 4 == 3:
        s = sqrt_p_3_mod_4(a, q)
    elif q % 8 == 5:
        s = sqrt_p_5_mod_8(a, q)
    gcd, c, d = egcd(p, q)
    x = (r * d * q + s * c * p) % n
    y = (r * d * q - s * c * p) % n
    lst = [x, n - x, y, n - y]
    print (lst)
    plaintext = choose(lst)
    string = bin(plaintext)
    string = string[:-16]
    plaintext = int(string, 2)
    return plaintext

## decide which answer to choose # 决定选择哪个答案
def choose(lst):
    for i in lst:
        binary = bin(i)
        append = binary[-16:]   # take the last 16 bits # 取最后 16 位
        binary = binary[:-16]   # remove the last 16 bits # 删除最后 16 位
        if append == binary[-16:]:
            return i
    return
## Find SQROOT in Zp where p = 3 mod 4 # 在 Zp 中查找 SQROOT，其中 p = 3 mod 4
def sqrt_p_3_mod_4(a, p):
    r = pow(a, (p + 1) // 4, p)
    return r

## Find SQROOT in Zp where p = 5 mod 8 # 在 Zp 中查找 SQROOT，其中 p = 5 mod 8
def sqrt_p_5_mod_8(a, p):
    d = pow(a, (p - 1) // 4, p)
    r =0
    if d == 1:
        r = pow(a, (p + 3) // 8, p)
    elif d == p - 1:
        r = 2 * a * pow(4 * a, (p - 5) // 8, p) % p
    return r
def egcd(a, b):
    if a == 0:
        return b, 0, 1
    else:
        gcd, y, x = egcd(b % a, a)
        return gcd, x - (b // a) * y, y

bits=60
msg="hello"
if (len(sys.argv)>1):
        msg=str(sys.argv[1])
if (len(sys.argv)>2):
        bits=int(sys.argv[2])
while True:
        p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
        if ((p % 4)==3): break
while True:
        q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
        if ((p % 4)==3): break
n = p*q
print ("=== Message ===")
print(("Message=%s") % msg)
print(("\n=== Private key (%d bit prime numbers) ===") % bits)
print(("p=%d, q=%d") % (p,q))
print("\n=== Public key ===")
print("n=%d" %  n)

plaintext =  bytes_to_long(msg.encode('utf-8'))

ciphertext = encryption(plaintext, n)
print("\nCipher:",ciphertext)
plaintext = decryption(ciphertext, p, q)
st=format(plaintext, 'x')
print(bytes.fromhex(st).decode())

128 位素数的示例运行 [here]:

=== Message ===
Message=hello

=== Private key (128 bit prime numbers) ===
p=270576397968349702240268570806789986947, q=219242991039694982252977037582947245671
=== Public key ===
n=59321978795327837368543975705006433832257716767865371948246597234695692256437
Cipher: 863473166557328969468694791968801
hello

你可以在此处尝试一些可证明安全的公钥加密：

Rabin public key \ \ import random from Crypto.Util.number import * import codecs import Crypto from Crypto import Random def…\ \ asecuritysite.com

参考文献

[1] Rabin, M. O. (1979). Digitalized signatures and public-key functions as intractable as factorization. (数字化签名和公钥函数与因式分解一样棘手。)

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～