最新MSM硬件实现方案的深入研究

ZPrize 2023 一等奖

作者：Tony Wu

简介

零知识证明 (ZKPs) 在计算上极其昂贵，其中多标量乘法 (MSM) 在许多 ZK 证明系统中占据主导地位。2023 年 ZPrize 竞赛（奖项 1A）要求参赛者加速 NVIDIA GPU 或 AMD FPGA 上的 MSM。

这篇博文中描述的工作是 ZPrize 2022 获奖者 Niall Emmart（来自 Yrrid Software）和 Ingonyama 的 Tony Wu 之间的合作。Niall 是该项目的架构师，Tony 负责实施。

为了在多个椭圆曲线上实现更高的性能，该团队首次在加速器平台上实现了用于椭圆曲线加法的 批量仿射 方法。这种方法显著降低了与 MSM 相关的计算负担，标志着基于硬件的 ZK 计算取得了显著进展。该设计的一些主要亮点：

• 能够在 U250 FPGA 上安装三个 EC-adder，比现有技术提高了 1.5 倍
• 在 BLS12–381 和 BLS12–377 曲线上的性能相同
• 在大多数 MSM 计算中实现了 >99% 的流水线效率

这篇博文深入探讨了实现的细节，概述了架构，并深入研究了使设计工作的关键组件。最后，我们讨论了对未来 ZK 硬件的影响，以及实现我们最终目标（端到端 ZK 加速）的下一步措施。

ZPrize 2023

今年竞赛的挑战（奖项 1A）包括使用 AMD Alveo U250 FPGA 卡 尽快计算一批大小为 2²⁴ 的四个 MSM。

AMD U250 FPGA

与去年的比赛相比，一个显著的变化是要求同时支持 BLS12–381 和 BLS12–377 曲线。以前，比赛只关注 Aleo 使用的 BLS12–377 曲线。在去年的比赛中，人们发现 BLS12–377 曲线可以映射到计算效率更高的“扭曲爱德华兹”表示。新的要求旨在更广泛地推进 MSM 处理的最新技术，因为 BLS12–381 缺乏扭曲爱德华兹表示。

多标量乘法

多标量乘法 (MSM) 是椭圆曲线密码学 (ECC) 中的一个基本运算。它涉及计算标量向量 𝑠 和椭圆曲线点向量 𝑃 的元素乘积之和。

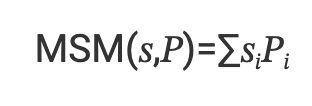
对于 BLS12–381，标量为 255 位宽，点的每个坐标为 381 位。这意味着当向量大小很大时（在我们的例子中为 2²⁴），MSM 的计算量非常大。

计算 MSM 最快的算法是桶方法（又名 Pippenger 算法），它通过将标量切分为 𝑚 个 𝑤 位的窗口，将问题分解为更小的 MSM。

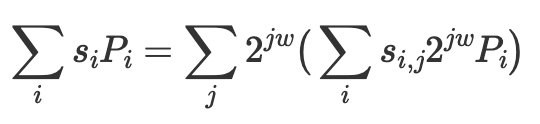
因此，我们可以并行计算 𝑚 个小的 MSM，然后将部分结果相加。

我们不会在这篇博客中更详细地描述桶方法，因为它是计算 MSM 的典型方式。更多信息请参见：

• 用于多标量乘法 (MSM) 的 Pippenger 算法
• zkStudyClub：多标量乘法：与 Gus Gutoski 一起探讨的最新技术和新想法

椭圆曲线加法

由于标量乘法定义为点的重复相加，因此 MSM 的主要计算成本是所需的大量椭圆曲线加法。因此，优化实现 EC-adder 所需的 FPGA 资源量非常重要。

仿射坐标中 ec-addition 𝑃+𝑄=𝑅 的公式为：

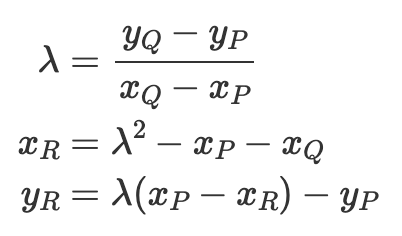
我们可以看到，为了计算 𝜆，我们需要执行除法。由于我们在素数域上运算，因此需要模逆运算，这非常昂贵。

因此，大多数先前的 MSM 设计选择将典型的 (𝑥,𝑦) 坐标（称为仿射坐标）扩展为扩展坐标，这用更多的乘法运算来换取除法运算。例如，使用扩展雅可比坐标 (𝑥,𝑦,𝑧𝑧)+(𝑥,𝑦)：

U2 = X2 * ZZ1
S2 = Y2 * ZZZ1
P = U2 - X1
R = S2 - Y1
PP = P2
PPP = P * PP
Q = X1 * PP
X3 = R2 - PPP - 2*Q
Y3 = R * (Q - X3) - Y1 * PPP
ZZ3 = ZZ1 * PP
ZZZ3 = ZZZ1 * PPP

批量仿射 EC-加法

有一种众所周知的方法称为 蒙哥马利技巧，可用于廉价地计算一批值的逆。也就是说，如果我们想计算 1/𝑎、1/𝑏、1/𝑐 和 1/𝑑，我们可以首先通过将它们相乘来 批量 输入：

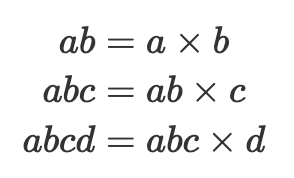
然后计算批量逆：

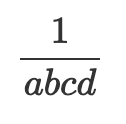
然后我们可以通过 解批处理 它们来获得各个逆：

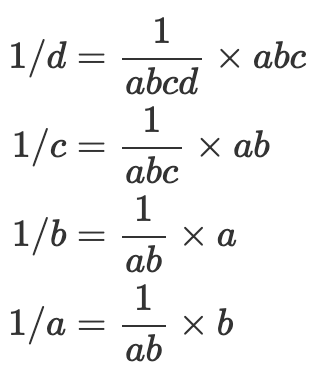
虽然这在理论上看起来很简单，但很难实现。这是因为这种公式没有考虑实现此目的所需的乘法器的延迟，也没有考虑必须保存以进行解批处理的所有中间值。

在我们的设计中，我们以蒙哥马利技巧的精神实现了批量仿射 EC-加法，但我们自己的两步批处理方法使其可以物理地在 FPGA 上实现。

架构概述

对于我们的设计，我们选择将标量切分为 21 个窗口，每个窗口 13 位。我们使用 带符号切片技巧 来将切片减少到只有 12 个物理位。

我们的设计包括以下关键组件：

• 一个主要的入口/出口单元，从设备内存中读取点和标量，并接收来自主机的启动 MSM 命令。
• 三个用于 EC-加法的计算单元 (CU)

\* 每个计算单元负责 21 个窗口中的 7 个，并且能够在每个时钟周期执行一个 EC-加法。

\* 每个计算单元包含 6 个模块化乘法器。

• 一个共享反相器，能够每时钟周期计算 3 个逆。

\* 反相器包含 2 个模块化乘法器。

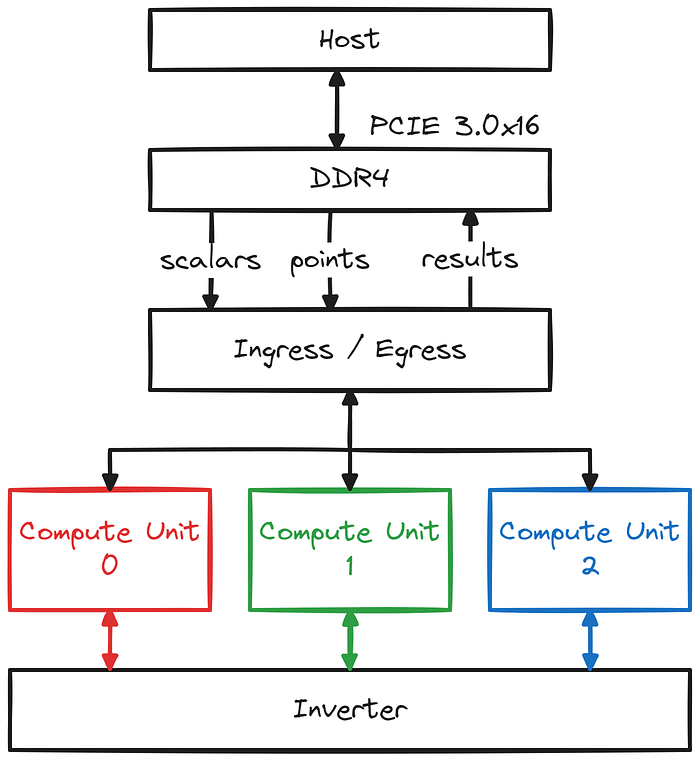
现在让我们看看数据流：

设置阶段

1. 主机使用我们的 BLS12–381 或 BLS12–377 设计对 FPGA 卡进行编程
2. 主机将 2²⁴ 个点传输到设备内存 (DDR4)。

计算阶段

注意：我们将引用诸如 42、336 和 1008 之类的魔术数字。这些数字是经过策略性选择的，同时考虑了我们设计的各种参数和约束，但是我们不会在这篇博客中详细介绍。

1. 主机将第一组标量传输到设备内存

\* (注意，我们可以将下一组标量传输与第一次执行重叠)

2. 入口单元从内存中读取标量和点的对，并将它们广播到三个计算单元。
3. 每个计算单元将 336 个 EC 操作批量处理在一起，然后将该批处理发送到共享反相器。
4. 反相器将批处理进一步聚合为包含 1008 个字段元素的单个批处理。
5. 对于每批 1008 个，反相器仅使用高度优化的扩展欧几里得算法执行 4 个实际反演。
6. 通过反向过程对逆进行解批处理，然后将其发回计算单元。
7. 最后，执行实际的 EC-加法，并将结果保存回各自的窗口内存中。

完成阶段

1. 一旦所有点和标量都被消耗完，所有窗口内存的内容将被发送回主机。
2. 主机计算最终总和并返回结果。

计算单元设计

放大计算单元，我们看到点-标量对首先流经 点标记器，它使用检索 ID 标记传入点，并将该点保存到缓存中。然后，标量流向 切片器，它将标量转换为桶索引和其他元数据。然后，这些元数据包被发送到它们各自的窗口通道。

在每个窗口通道中，元数据包首先进入 冲突处理程序，该处理程序旨在避免桶冲突。当一个 EC 操作尝试访问与仍在进行中的较早操作（即，结果尚未写回）相同的桶时，就会发生冲突。冲突处理程序会尝试通过重新排序来自切片器的操作来避免冲突。当桶正在进行中时，桶会被标记为 锁定，而当桶被写回时，会被标记为 解锁。当检测到访问锁定的桶时，冲突处理程序会尝试将新操作与不再冲突的先前挂起操作进行交换（即，它寻址的桶已被解锁）。冲突操作被保存到挂起缓冲区中，而非冲突操作被转发到流水线中，到达窗口内存。在我们的模拟中，我们看到在整个 MSM 计算过程中，挂起缓冲区中的操作数量稳定在 35 个条目左右（同时假设一个操作将处于运行状态约 3500 个时钟周期）。

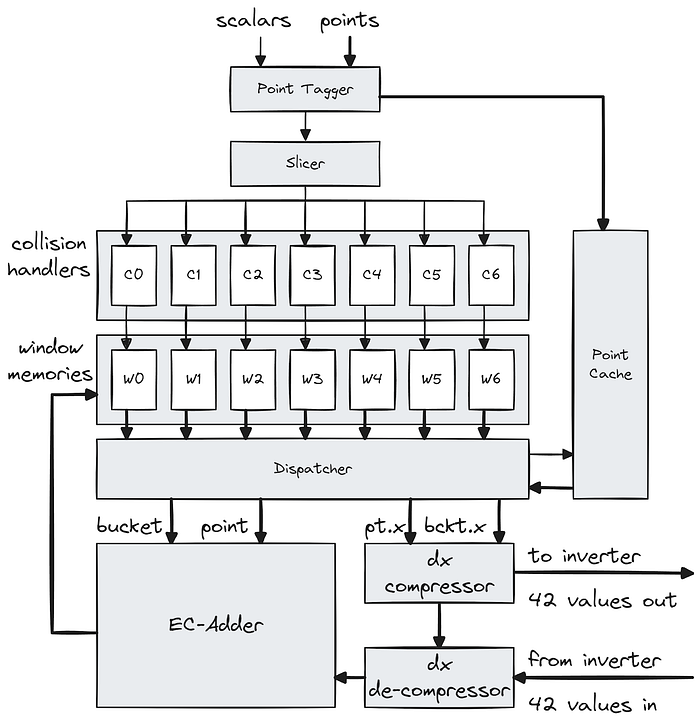
计算单元设计

在索引并检索其各自的桶值之后，操作将等待由 调度程序 按轮询顺序进行调度。在调度期间，元数据中包含的检索 ID 用于从缓存中检索相关点。这种点缓存方法非常重要，因为它使我们不必在通过冲突处理程序的每个 EC 操作中保留该点的单独副本，否则将导致 7 倍的内存使用量。一旦一个 ID/标签被访问了七次，缓存条目将被释放，并且该 ID 可以被重用。

调度后，点 (𝑃) 和桶 (𝑄) 将排队到 EC-adder 的输入端，并且它们的 x 坐标被馈送到 dx 压缩器，这是计算批量反演的第一阶段。我们首先计算分母，dx = xᵩ — xₚ。然后，我们将 336 个分母（𝑑𝑥 的分母）批量处理在一起，并将此数据视为 8 个向量，每个向量包含 42 个元素：

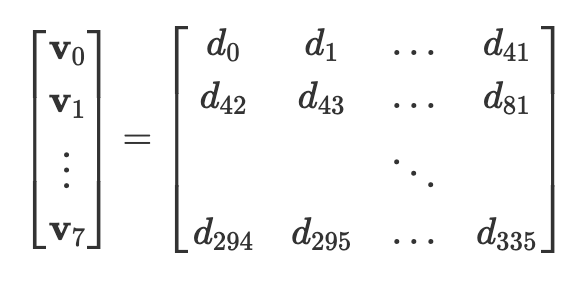
dx 压缩器按元素顺序将 8 个向量相乘，以生成一个长度为 42 的向量，计算：

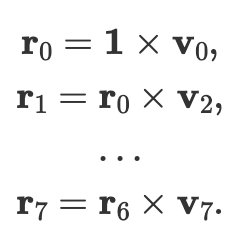
这是通过按顺序将向量元素馈送到乘法器中来完成的，该乘法器将结果重新用作第二个输入操作数。这是我们批处理/压缩过程的第一步，并且在每个计算单元中本地完成。然后，将最终的 42 个产品发送到共享反相器，同时保存中间产品以供解批处理/解压缩过程中使用。

注意：这意味着我们的乘法器的延迟必须小于 42 个周期才能有效（即，无停顿）。

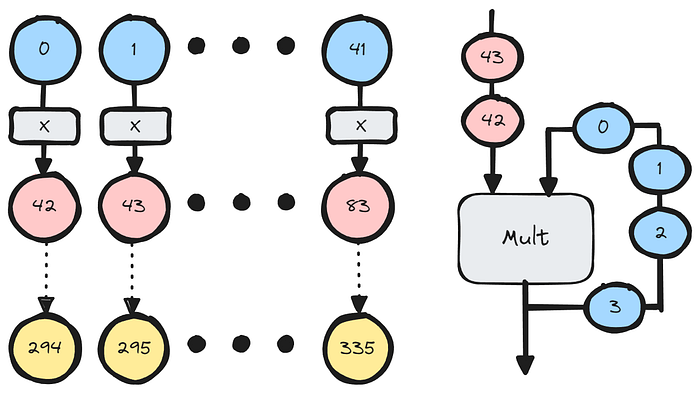
向量压缩（dx 压缩器）

当 42 个逆返回时，将使用压缩器产生的中间产品将其解压缩回 336 个逆。然后，这些逆允许 EC-adder 执行并将结果写回窗口内存。

反相器设计

现在放大到共享反相器，我们看到它从三个计算单元中的每个单元接收 42 个字段值，并使用树状结构将 126 个字段元素进一步压缩为仅 4 个字段元素。

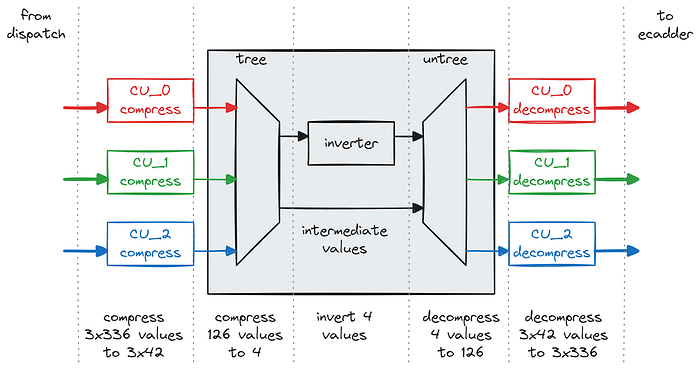
反相器设计

下图显示了我们将如何将 8 个字段元素压缩为 2 个字段元素的迷你示例。在下面，我们假设我们有元素 𝑎,𝑏,𝑐,𝑑,𝑒,𝑓,𝑔,ℎ，并且我们将它们视为两个二叉树的叶节点。叶节点的父节点通过子节点的乘积来计算，并且这种计算会以递归方式一直持续到根节点。为了能够解压缩批量逆 (1/𝑎𝑏𝑐𝑑, 1/𝑒𝑓𝑔ℎ)，我们需要保存所有中间节点的值。

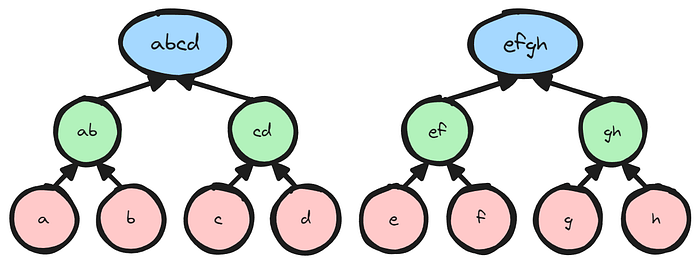
树压缩

反转后，我们从根节点开始，然后逐步返回到单个逆。在每个节点，我们可以通过乘以先前保存的右子节点来派生左子节点。类似地，我们可以通过乘以先前保存的左子节点来派生右子节点。

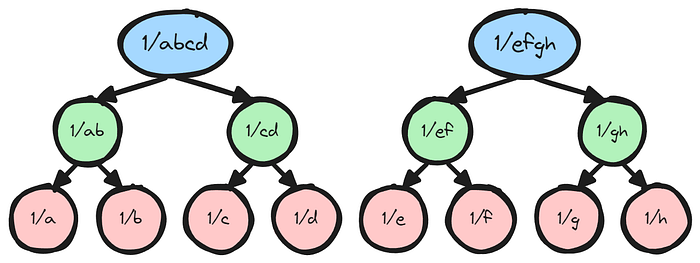
树解压缩（Untree）

在完整的情况下，我们有 126 个叶节点和 4 个根节点。我们选择压缩为并反转 4 个字段元素而不是 1 个字段元素的原因再次是由于我们乘法器的延迟。

我们在反相器内部使用两个完全流水线的乘法器，一个用于压缩器树，另一个用于解压缩器 untree。通过完全流水线化，我们的意思是每个乘法器可以每个周期处理一次乘法，但是结果不会立即可用。当输入呈现时和当对应的输出准备就绪时，时钟周期之间存在一定的延迟。当我们处理树的各层时，我们可以用来填满流水线的并行操作越来越少。因此，当我们接近根时，我们的处理效率会降低，并且我们确定如果我们一直压缩到一个根，实际上会降低我们的反相器吞吐量。

乘法器

由于我们的一些乘法器对低延迟有要求，因此我们试验了几种乘法器设计。我们提出了三种针对不同目的优化的乘法器设计：

• 低延迟乘法器 (LL)

\* 延迟：250MHz 时为 22 个周期 - 400MHz 时为 38 个周期

\* DSP：413

\* LUT：约 24K

• 中等面积乘法器 (MA)

\* 延迟：>42 个周期

\* DSP：372

\* LUT：约 27K

• 低面积乘法器 (LA)

\* 延迟：>80 个周期

\* DSP：346

\* LUT：约 38K

最后，我们只使用了 LL 乘法器和 MA 乘法器。我们确定，虽然使用 LA 乘法器会节省我们更多的 DSP，但它会造成更多的路由拥塞，并会延长编译时间。

结果

我们已将 BLS12–377 和 BLS12–381 设计提交给 ZPrize。两种设计都以 250MHz 的时钟频率运行，实现了 每秒 7.5 亿次 EC 操作。这使我们的设计能够在 2.04 秒 内计算一批四个 2²⁴ MSM ！这是一个重要的成就，尤其是对于不存在扭曲爱德华兹表示的 BLS12–381 而言。此结果比去年仅支持 BLS12–377 的 ZPrize 获奖者快 2.5 倍（调整为 2²⁴）。

下图显示了我们的三个计算单元在 FPGA 上的物理映射。

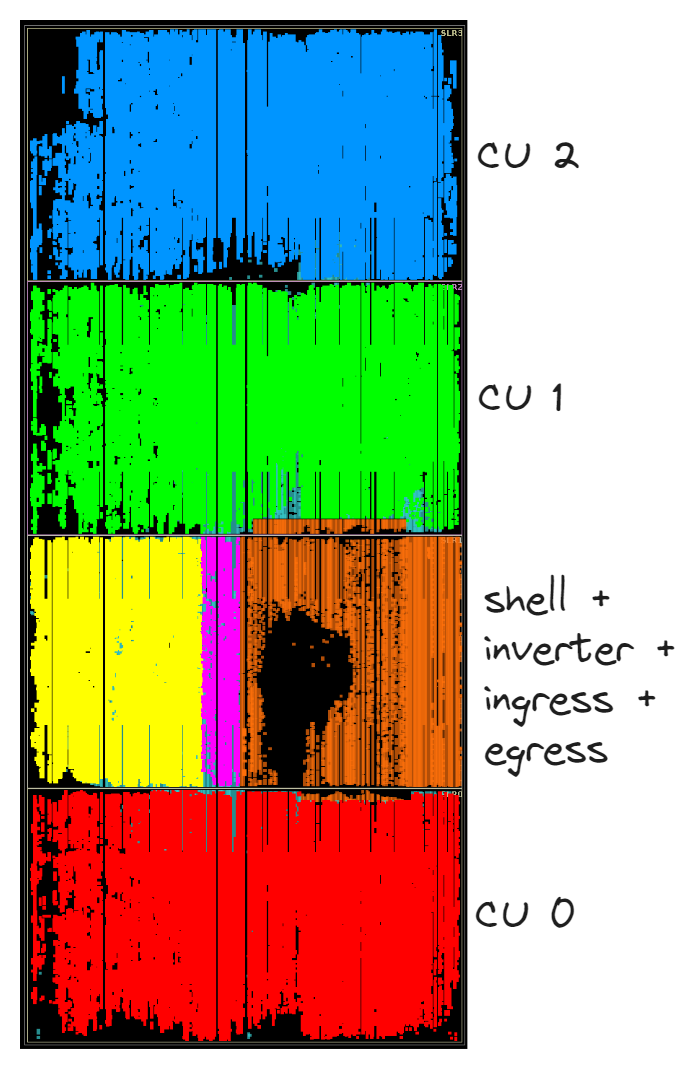
如下表所示，我们的总资源使用率非常低。这意味着绝对还有增长空间！虽然我们没有足够的 DSP 资源来实例化另一个计算单元，但我们可以将 LUT 和 FF 预算用于积极的流水线化以提高时钟频率。

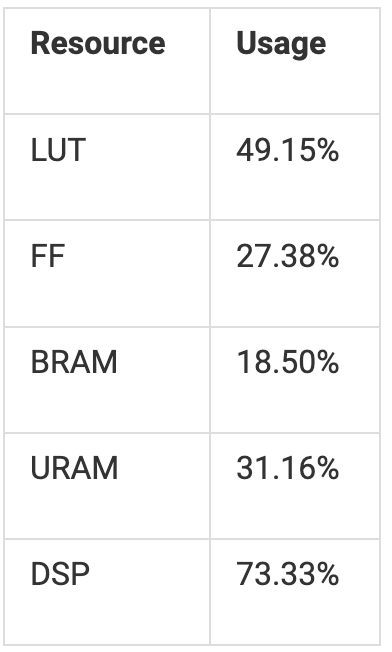
另一个有趣的注意事项是我们的功耗仅为 120W，其中 85W 用于 MSM 计算，35W 用于 shell（包括 DDR4 和 PCIe 基础设施）。这意味着我们在 225W 卡上拥有充足的功率裕量。如果我们提高计算频率，我们预计 MSM 部分的功耗会随着频率线性增加，而 shell 功耗将保持大致相同。

凭借充足的资源和功率裕量，我们有信心只需少量工作即可将频率提高到 400MHz。这将使性能进一步提高 1.6 倍，从而实现 每秒 12 亿次 EC 操作。

一个阻碍潜在性能的方面是提供的 FPGA 卡上缺少 HBM（高带宽内存）。如果具有足够的带宽，我们将能够使用更大的窗口大小，就像在 GPU 上通常所做的那样。这将大大减少计算 MSM 所需的 EC 操作数量。

结论

我们很高兴展示在硬件中实现的批量仿射 EC-加法的第一个示例。借助提供的 FPGA 设计，我们现在已经在性能的有效范围内，而这种性能目前只能在高端 GPU 上实现。

我们应该记住，U250 FPGA 卡于 2018 年发布，基于 TSMC 16nm 工艺。我们期待 AMD 即将推出的基于 7nm 和 3nm 的卡，这将大大提高性能。我们特别期待的一项功能是片上网络，它在 AMD 的 Versal 设备上可用，这将大大简化我们设计中遇到的复杂的数据移动。

此外，我们容忍延迟的设计为探索有趣的新途径开辟了道路。例如：在 AMD 的 Versal 设备中使用高延迟 AI 引擎，并将 GPU 的原始计算能力与 FPGA 的灵活性相结合，以进一步加速。

最后，这将我们引向异构计算。零知识证明不仅仅涉及 MSM，还需要加速大量操作才能实现端到端加速。CPU 和加速器以集成的异构方式协同工作非常重要。我们已经看到主要的硬件供应商推出了异构计算机，例如 Nvidia 的 Grace-Hopper、AMD 的 MI300A 和 Versal 产品。迈向端到端 ZK 加速！

请观看我们在 ZK-Accelerate Athens 与 AMD 的 @hamid_r_salehi 的联合演示！

AMD 的 Hamid Salehi 和 Ingonyama 的 Tony Wu 展示了 ZPrize '23 及其对未来 ZK 硬件的影响

Ingonyama

•

关注 Ingonyama

Twitter：https://twitter.com/Ingo_zk

YouTube：https://www.youtube.com/@ingo_zk

GitHub：https://github.com/ingonyama-zk

LinkedIn：https://www.linkedin.com/company/ingonyama

加入我们：https://www.ingonyama.com/career

• 原文链接： medium.com/@ingonyama/de...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～