隐私货币:第二部分
- bhargav
- 发布于 2024-05-22 20:34
- 阅读 761
本文介绍了理解Project Tachyon中集合非包含累加器的先决数学知识,回顾了群论、循环群以及离散对数问题在密码学中的应用。同时,文章详细解释了Pedersen承诺方案的隐藏和绑定特性,并展示了如何在Rust中实现这些承诺,最后说明了Pedersen承诺在隐私保护协议和简洁证明中的应用。
⚠️ 警告: 数学内容。这是一篇相当技术性的文章!我假设读者对高中数学有扎实的理解,并且愿意耐心阅读 :)
这篇博客回顾了理解 Tachyon 项目 中的 set-noninclusion accumulator 所需的预备数学知识——如果你已经熟悉基本的抽象代数,可以跳到下一篇文章。
一些数学预备知识
音乐的动机
18 世纪,作曲家 约翰·塞巴斯蒂安·巴赫 创作的音乐因其优雅和结构而备受赞赏。尽管缺乏正规的数学训练,巴赫的作曲往往具有一种内在的数学精确性。一个引人注目的例子是他《音乐的奉献》中的 卡农曲:
J.S. Bach - Crab Canon on a Möbius Strip
巴赫《音乐的奉献》中的卡农曲是一个迷人的数学音乐案例。当正向和反向同时演奏时,它会创造出一个完美的 palindrom——一个音乐莫比乌斯带,其中结尾无缝地连接到开头。这种拓扑结构,通过扭曲和连接一个条带创造出一个单面表面,反映了卡农的旋律如何在保持音乐连贯性的同时,在两个方向上被读取。
音乐表达和隐藏结构之间的联系长期以来一直吸引着人们。这里的一个关键思想是 五度循环 ——一个将音符布局成环状的图表,使得密切相关的音调彼此相邻。这是一种理解和谐的便捷方法,其圆形形状暗示了声音之下更深层次的东西:一种音乐遵循的模式,即使我们没有有意识地意识到它。
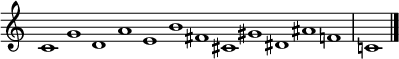 你的浏览器不支持audio标签。
你的浏览器不支持audio标签。
顺时针五度循环在一个八度音阶内。来源:Wikipedia。
在此基础上,现代可视化让我们将音乐运动视为某种几何形状。在下面的动画中,一个大七和弦进行在脐状环面的表面上移动——一个循环的、扭曲的形状,展示了和谐如何在循环的同时向前移动。就像巴赫的卡农一样,它将音乐变成了不仅仅是一行音符——它变成了一种在空间中运动,由我们可以开始识别的模式和规则塑造,即使我们还不能命名它们。
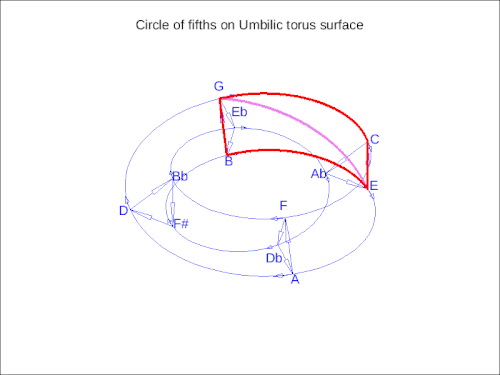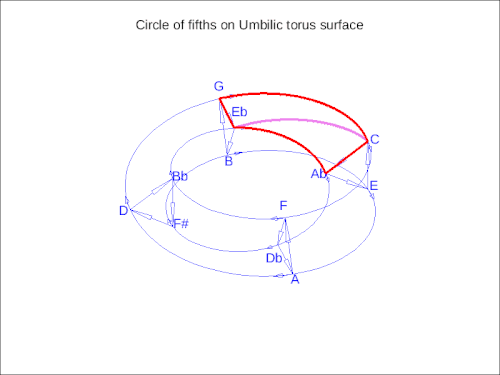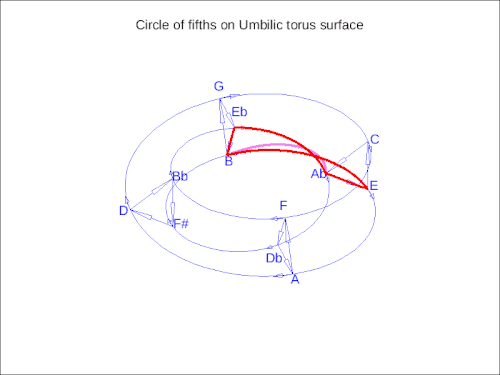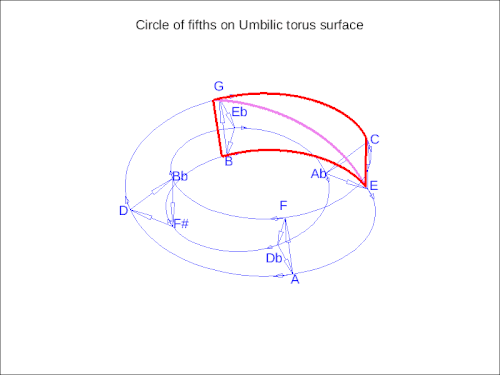
这个动画展示了一个在脐状环面表面上追踪的大七和弦进行——一个五度循环的更高维度可视化。通过谐波空间的平滑旋转代表了音调运动作为连续几何,揭示了音高、音程和曲率之间的深刻对称性。
这些模式不仅仅是美丽的——显然,在表面之下还有更深层次的东西。为了真正理解它,我们需要一种新的语言——一种帮助我们谈论音乐如何移动、转换和循环回到自身的方式。这就是我们接下来要讨论的内容:群论。
从循环到逻辑
群 是一个配备了组合元素的规则(一个操作)的集合,该规则的行为是可预测的:有一种组合任意两个元素的方法(封闭性),元素的分组方式无关紧要(结合律),存在一个什么都不做的单位元素(单位元),并且每个元素都有一个撤消它的逆元素(逆元)。
群的一个简单例子是有限循环群 Z/nZ\mathbb{Z} / n \mathbb{Z}Z/nZ,即模 nnn 的整数,它由集合
0,1,2,…,n−1 {0, 1, 2, \ldots, n - 1}0,1,2,…,n−1
组成,其运算是模 nnn 加法。例如,在 Z/12Z\mathbb{Z} / 12 \mathbb{Z}Z/12Z 中,12≅012 \cong 012≅0,所以 7+6=1mod127 + 6 = 1 \mod 127+6=1mod12。查看 Wikipedia 以获取群的数学定义。
事实证明,循环群对于密码学也非常有用。假设你从 Z/12Z\mathbb{Z} / 12 \mathbb{Z}Z/12Z 中的 000 开始,并不断地加 5。那么你会得到以下序列:
0,5,10,3,8,1,… 0, 5, 10, 3, 8, 1, \ldots0,5,10,3,8,1,…
最终,你会到达集合中的每个数字。现在,如果我问你,你必须加多少次 5 才能得到数字 8,你能告诉我吗?
这就是 离散对数问题。给定一个生成器(如 5)和一个结果(如 8),挑战在于找出生成器被应用了多少次。在这个例子中,答案是 4,因为 5×4=20≅8mod125 \times 4 = 20 \cong 8 \mod 125×4=20≅8mod12。
在密码学中,我们经常使用 乘法表示法 来书写循环群,其中重复应用生成器 ggg 被写成:
g0,g1,g2,…,gn−1g^0, \; g^1, \; g^2, \; \dots, \; g^{n - 1}g0,g1,g2,…,gn−1
如果 ggg 是生成器,这将给出群的所有元素。
离散对数问题 问: 给定 ggg 和 h=gxh = g^xh=gx,找到 xxx。
对于小数字,这很容易通过试验来解决。但在大型循环群中(尤其是那些由数百位数的素数构建的循环群),这个问题变得极其困难。对于小数字,这很容易通过试验来解决。但在大型循环群中(比如以太坊的 BLS 签名中使用的那些,其中模数是一个 381 位的素数),这个问题实际上是不可能逆转的,而这正是它能够安全地抵御 经典计算机 的原因。
Pedersen 向量承诺方案
最后,我们有了可以谈论依赖于群结构来确保 隐藏性 和 绑定性 的工具的语言:密码学承诺的两个基本属性。一个最简单和最优雅的例子是 Pedersen 承诺。
隐藏性和绑定性
在进一步深入之前,值得停下来解释一下我们所说的 隐藏性 和 绑定性 是什么意思。
-
隐藏性 意味着承诺不会泄露关于底层消息的任何信息。即使有人看到承诺,他们也无法知道承诺的值——因为它被使用随机性掩盖了。
-
绑定性 意味着一旦你承诺了一个值,你就不能再改变你的想法。也就是说,你不能用不同的值打开相同的承诺。这确保了承诺是固定的,并且在事后无法更改。
简而言之:隐藏性保护隐私;绑定性确保完整性。
Pedersen 承诺
设 GGG 为素数阶 qqq 的循环群,生成元为 ggg 和 hhh,使得没有人知道它们之间的离散对数。为了承诺一个值 m∈Z/qZm \in \mathbb{Z} / q \mathbb{Z}m∈Z/qZ,选择一个随机的 masking factor r∈Z/qZr \in \mathbb{Z} / q \mathbb{Z}r∈Z/qZ 并计算:
Com(m,r)=gmhr\text{Com}(m, r) = g^m h^rCom(m,r)=gmhr
这是对 mmm 的承诺,它:
- 完美隐藏:因为 rrr 是随机选择的,输出不会泄露关于 mmm 的任何信息
- 计算上绑定:在离散对数假设下,找到两个不同的对 (m,r)(m, r)(m,r) 和 (m′,r′)(m', r')(m′,r′) 产生相同的承诺是不可行的
此外,Pedersen 承诺是 同态的:
Com(m1,r1)⋅Com(m2,r2)=Com(m1+m2,r1+r2)\text{Com}(m_1, r_1) \cdot \text{Com}(m_2, r_2) = \text{Com}(m_1 + m_2, r_1 + r_2)Com(m1,r1)⋅Com(m2,r2)=Com(m1+m2,r1+r2)
这意味着承诺可以在不打开它们的情况下相加,这个属性在许多协议中很有用。
现在,下面是我们在 Rust 中如何实现它:
pub fn commit(m: Scalar, r: Scalar, g: GroupAffine, h: GroupAffine) -> GroupAffine {
(g * m + h * r).into_affine()
}从承诺到向量承诺
为了承诺一个完整的向量 m=(m1,m2,…,mn)\mathbf{m} = (m_1, m_2, \dots, m_n)m=(m1,m2,…,mn),我们通过使用 nnn 个独立的生成器 g1,g2,…,gn∈Gg_1, g_2, \dots, g_n \in Gg1,g2,…,gn∈G 和一个单独的 masking 基 hhh 来扩展这个想法。承诺是:
Com(m,r)=g1m1⋅g2m2⋯gnmn⋅hr\text{Com}(\mathbf{m}, r) = g_1^{m_1} \cdot g_2^{m_2} \cdots g_n^{m_n} \cdot h^rCom(m,r)=g1m1⋅g2m2⋯gnmn⋅hr
Rust 中的向量承诺版本采用一个生成器数组:
pub fn open(v: &[Scalar], r: Scalar, j: usize) -> Result<(Scalar, Scalar, GroupAffine)> {
if j >= v.len() {
return Err(anyhow!("Index out of bounds")); // 索引越界
}
let blind = POINTS[0] * r;
let witness = POINTS[1..].iter().enumerate()
.filter(|(i, _)| *i != j)
.map(|(i, p)| *p * v[i])
.sum::<GroupProjective>() + blind;
Ok((v[j], r, witness.into_affine()))
}这紧凑地将整个向量 m\mathbf{m}m 绑定到一个单独的群元素中。它保持了相同的属性:
- 隐藏性,因为随机的 rrr 掩盖了整个向量
- 绑定性,假设生成器 g1,…,gng_1, \dots, g_ng1,…,gn 是独立的,并且它们之间的离散对数关系是未知的
这是如何验证承诺:
pub fn check(c: GroupAffine, v_j: Scalar, witness: GroupAffine, h_j: GroupAffine) -> bool {
c == witness + h_j * v_j
}代数属性
Pedersen(向量)承诺特别强大的是它们的代数结构:
-
线性性:承诺尊重线性组合: Com(m,r)⋅Com(m′,r′)=Com(m+m′,r+r′)\text{Com}(\mathbf{m}, r) \cdot \text{Com}(\mathbf{m}', r') = \text{Com}(\mathbf{m} + \mathbf{m}', r + r')Com(m,r)⋅Com(m′,r′)=Com(m+m′,r+r′) 其中向量加法是按分量进行的。
-
可扩展性:你可以聚合多个向量的承诺: ∏i=1kCom(m(i),ri)=Com(∑i=1km(i),∑i=1kri)\prod_{i=1}^k \text{Com}(\mathbf{m}^{(i)}, r_i) = \text{Com}\left(\sum_{i=1}^k \mathbf{m}^{(i)}, \sum_{i=1}^k r_i\right)i=1∏kCom(m(i),ri)=Com(i=1∑km(i),i=1∑kri)
-
内积兼容性:由于指数运算在和上是可分配的,Pedersen 承诺可以在内积参数中使用(如在 Bulletproofs 中),其中证明者和验证者都可以在不知道底层消息的情况下,以代数方式操作承诺。
-
非交互式开启证明:给定 m\mathbf{m}m 和 rrr,开启承诺并证明其正确性是微不足道的。如果需要,可以在顶层分层零知识变体。我们将在下一篇博客中看到这一点。
这些代数属性使 Pedersen 承诺成为隐私保护协议、SNARK 友好的构造以及大型数据集上的简洁完整性证明中最受欢迎的构建块。我们将在下一篇博客文章中看到我们如何构建 Sean Bowe 的 set-noninclusion accumulator。
- 原文链接: bhargav.wtf/blog/zcash-p...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 以太坊协议研究学习小组 - 2026 启动 67 浏览
- 神奇的 Zig、C 和 OpenSSL 117 浏览
- Shamir份额的魔力:BLS门限签名 367 浏览
- zkMesh:2026年1月回顾 388 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 387 浏览
- ZK 编年史:电路(第二部分) 391 浏览
- 有限域之美与力量 (以及 Zig) 485 浏览
- 扳手攻击:发生与预防 521 浏览
- zkEVM 安全性概览 584 浏览
- 基于哈希函数的签名(三):多次签名 663 浏览
- 基于哈希函数的签名(二):少量次数签名 828 浏览
- Zig 签名(Ed25519 和 ECDSA) 1169 浏览

