多值函数的图像保持定理
- RareSkills
- 发布于 2025-11-12 18:14
- 阅读 2098
本文介绍了图像保持定理,它是数论变换(NTT)的核心概念。该定理指出,对于多值函数,在特定条件下的图像与原始函数在不同定义域上的图像相同。通过重复取平方根来计算单位根,并展示了如何利用该定理来优化多项式求值,为后续章节中利用平方根扩展评估多值函数奠定基础。
我们将以一个不寻常的提示开始本章 —— NTT 算法非常简单,可以用不到 20 行代码实现。然而,使其工作的关键思想,奇怪的是,没有正式的数学名称。因此,我们将自由地给这个我们认为算法背后的核心定理,起一个(主观上)朗朗上口的名字:
多值函数的图像保持定理
为了解释图像保持定理,我们将回顾最后一个(非常简单的)关于单位根的概念,然后介绍该定理。
-th 嵌套平方根的根
“k 次单位根”的字面定义是单位根 满足 。换句话说:
因此,如果 是本原 4 次单位根,那么
应该不足为奇。
现在,如果 是本原 8 次单位根,我们来做同样的操作。结果将是
1 的 8 次方根生成所有 8 次单位根:
这些观察仅仅是定义问题。当然,我们不想直接计算 1 的平方根。首先找到本原 -th 单位根,然后生成 的答案集要容易得多。例如:
import galois
Fq = 17
k = 8
assert (Fq - 1) % k == 0, "no such subgroup"
GF = galois.GF(Fq)
pr = GF.primitive_root_of_unity(k)
roots = []
for i in range(0,k):
roots.append(pr**i)
print(roots)我们还可以观察到:
等等。如上所述,直接计算 是没有效率的。相反,我们考虑下面的图,其中每个向下的箭头都是它上面数字的平方根:
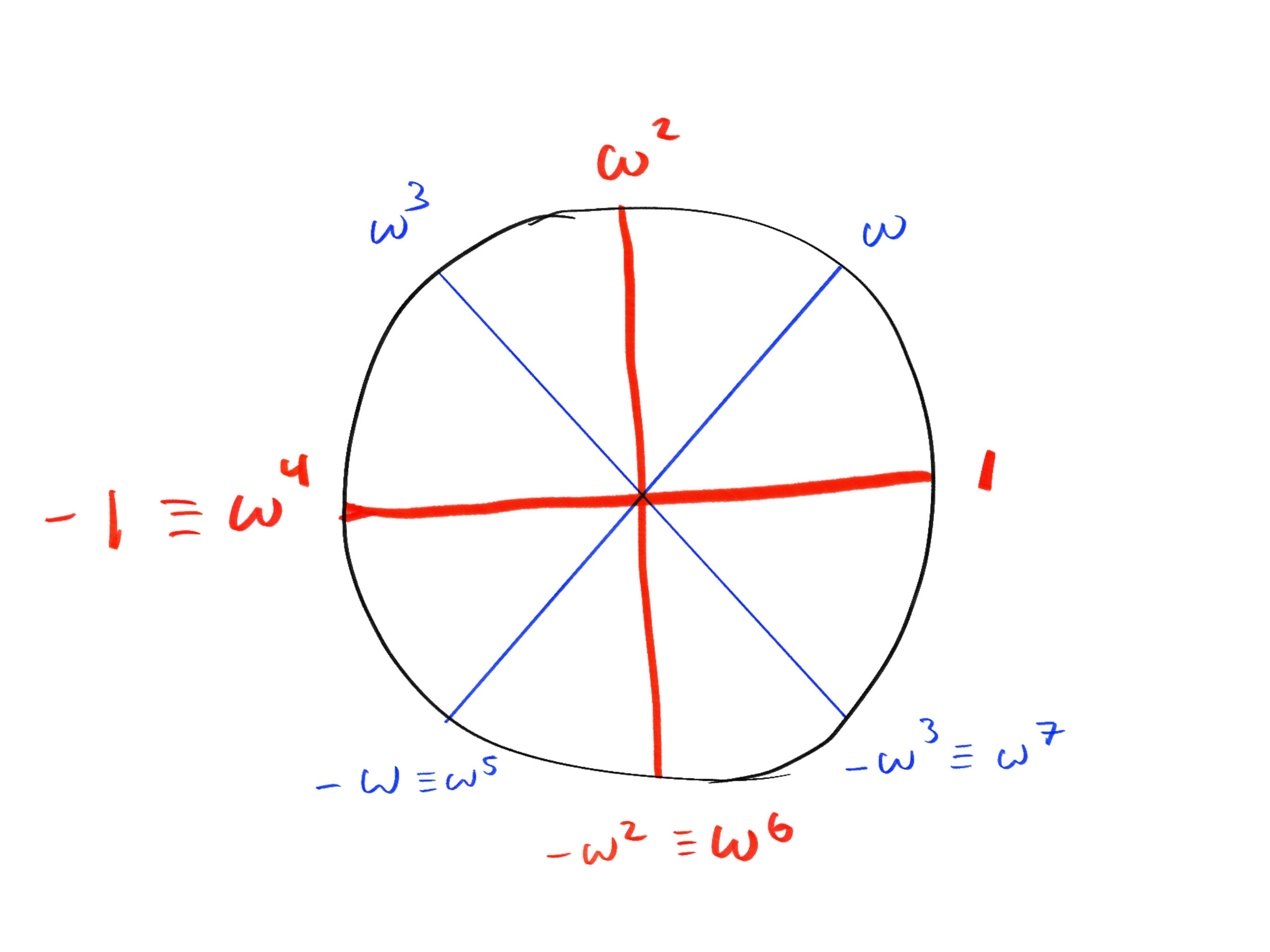
我们可以从 1 开始,通过重复取平方根来计算 8 次单位根。
对于任意 ,该图如下。
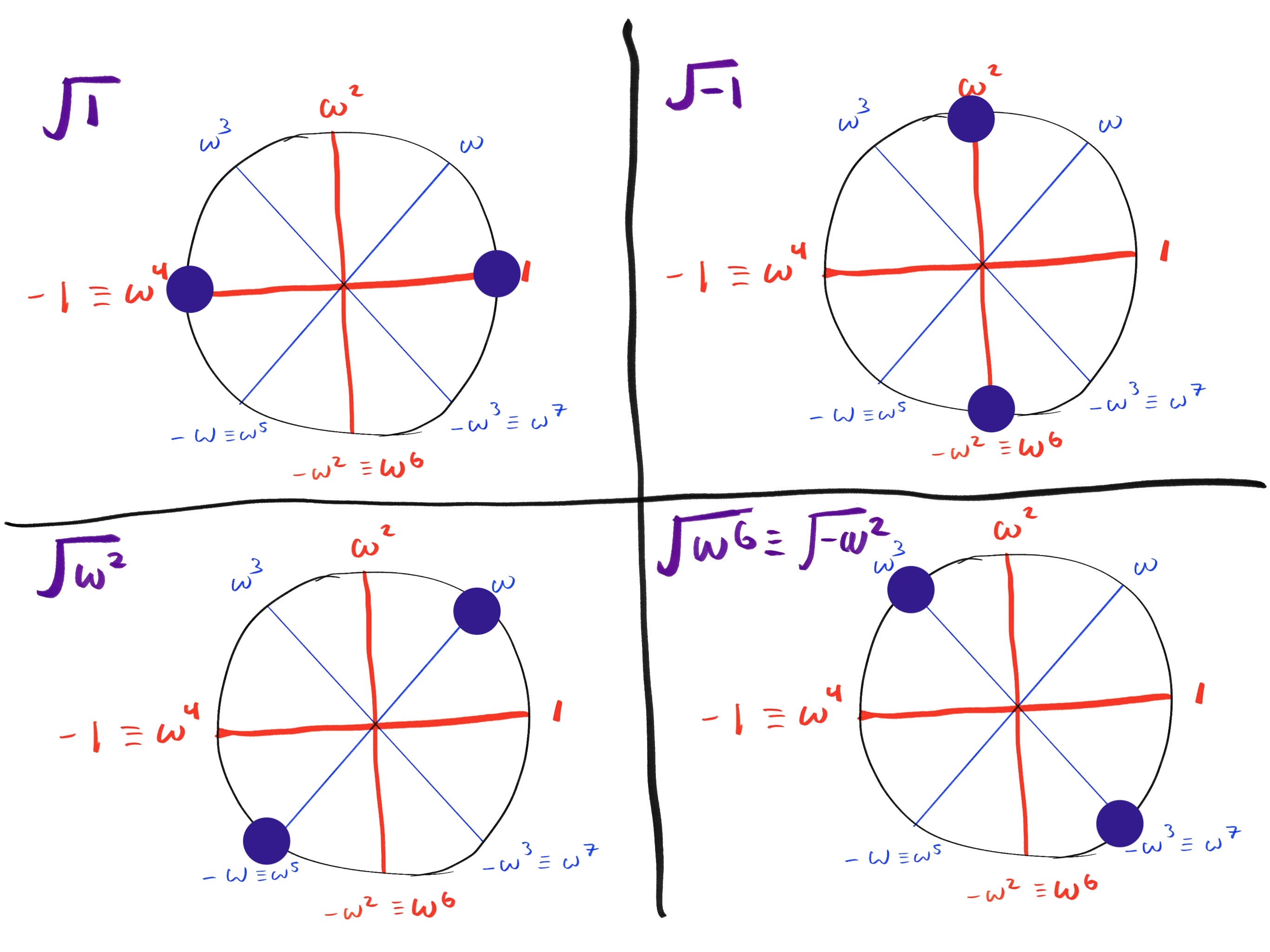
以下是平方根计算的演练:
1 的平方根是 。 与 -1 同余
回想一下前一章, 的平方根是 和 (假设 是偶数)。
因此, 的平方根是 。
另请注意, 的加法逆元是 。
因此,为了计算 没有负号,我们计算 。所以 的平方根是 。
的平方根是 。同样,为了去掉负号,我们计算
为什么 的平方根留给读者作为练习。
树的高度是
通过重复取 1 的平方根来计算 -th 单位根创建了一个高度为 的“树”。
概念化树的中间状态
集合
在数学上等价于 8 次单位根。集合也等价:
这也等价于:
换句话说:
快速说明 - 多值函数和图像
诚然,我们上面所做的观察结果仅仅是 -th 根定义的简单扩展。这些观察结果更有趣的含义将在以下章节中展示。但是,首先介绍一些数学术语将会有所帮助:
函数的像——如果我们有一组点,我们对一个函数求值,那么这组求值就是像。例如,如果函数是 ,我们在其上求值 的域是 ,那么像将是 。函数的值域是指函数可以输出的值的集合。在我们的上下文中,函数的像是指给定的一组输入的实际输出集合。
多值函数——一个函数,对于域中的单个点,可能返回多个评估结果。例如, 在 0 上求值为 0,但在 1 上求值为 。
注意:多值函数 的图像大于它的域。
考虑到这些定义,读者应该理解以下陈述:
“ 在域 上的像是 ”
“多值函数 在域 上的像是 ”
现在我们得到了一组更有趣的观察结果。
在 上求值的像 与 在 上求值的像相同 (k = 8)
这个说法是对上面展示的概念的简单改述,所以我们不再赘述。有趣的部分是我们如何将它推广到其他函数。
这里的细微之处在于 是一个返回八个元素的多值函数。
在 4 次单位根上求值的像 与在 上求值的多值函数 相同 (k = 4)
记住,所以 。这与在每个单位根上逐个求值 的图像相同。自从
读者练习:设 。 在 4 次单位根上的像是什么?在域 上多值函数 的像是什么?
在接下来的章节中,我们将展示如何处理更复杂的情况,例如 ,但现在,我们将展示如何实际计算我们在此处展示的简单情况的多值函数。但首先,让我们对我们目前为止所做的关于图像等价的观察给出一个正式的定义。
在 4 次单位根上求值的像 与 在二次单位根上求值的多值函数 相同 (k = 4)
这个例子与上面的例子非常相似,只是我们没有“定位”域 ,而是 。
我们有
这与在 上求值的图像相同
总而言之,如果我们将域“缩小” 因子 ,并将 中的每个 替换为 以创建一个新的多值函数 ,那么 和 的图像是相同的。
我们现在将正式定义我们一直在说明的概念
NTT 的核心定理:多值函数的图像保持定理
设 是本原 -th 单位根, 是 中定义的 -th 单位根。
设 是 2 的幂。
设 是 中的多项式。 设 是小于或等于 的 2 的幂。
设 是一个多值函数,通过将 中的每个 替换为 来创建。
设域 为 。 注意,如果 那么 。
在 上的像 与 在 上的像完全相等。
读者理解以上定理至关重要,因为它是数论变换所依赖的关键概念!
以下是一些例子,以加强这个概念:
- 在 4 次单位根上的 像是等于 在二次单位根上的像(如上一节所示)。
- 在 16 次单位根上的像是等于 在 8 次单位根上的像
- 在 k 次单位根上的像是等于 在 k/2 次单位根上的像
- 在 k/2 次单位根上的像是等于 在 k/4 次单位根上的像
以下部分显示了 的示例,其中 稍微复杂一些。
的图像保持定理示例
设 且域 为 4 次单位根 。
设 是多值函数 且域 为 或等效地 。
设 是多值函数 且域 为
, 和 的图像是相同的:
与 NTT 的连接
记住,NTT 的目标是在 时间内在 -th 单位根上评估 。换句话说,我们想要计算 在 -th 单位根上的像。
你可能可以猜到接下来会发生什么。
计算 在 -th 单位根上的像等同于计算一个新函数 的像,该函数的定义使得对于 中的每个 , 在 上求值。
但是,这留下了一个悬而未决的问题:
将 扩展到 并不能直接导致加速。从算法上讲,将 扩展到 -th 单位根与在 个点上评估 相同。这种评估 的替代方法如何帮助我们?
在下一章中,我们将演示如何使用平方根展开来评估多值函数,并解释这种方法如何防止冗余计算。
- 原文链接: rareskills.io/post/image...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Fiat-Shamir 启发式非交互式零知识证明之美(以及 Zig) 583 浏览
- 有限域之美与力量 (以及 Zig) 517 浏览
- ZK 编年史:数学基础 1569 浏览
- ZK编年史:Sum-Check 1364 浏览
- FFT友好的有限域 992 浏览
- 格密码学基础(四):多项式环上的加密 961 浏览
- 单位根的可视化表示 2245 浏览
- 单位根的平方根 2148 浏览
- k次单位根的平方是k/2次单位根 2089 浏览
- 单位根的 k/2 次幂等于 1 或 -1 2078 浏览
- 手动实现数论变换算法 2058 浏览

