单位根的可视化表示

如果 是一个 -th 单位根，那么 和 是加法逆元的性质可能看起来有点抽象——本章介绍了一种可视化方法，使这个概念更容易记住。

回想一下，-th 单位根是通过取本原 -th 单位根 并将其提升到连续幂来生成的。例如，如果 ，我们计算第 4 个单位根为

如果我们继续下去，指数将以模 4 环绕：

• （根据作为 4-th 单位根的定义）

等等。

请注意，指数在四的每个倍数处“环绕”。因此，对于任何 和 ，。由于 在我们的例子中，我们有

现在回想一下，模 的加法可以表示为一个“时钟”。这里，我们的时钟由“小时标记”0、1、2、3 组成，它们是的指数

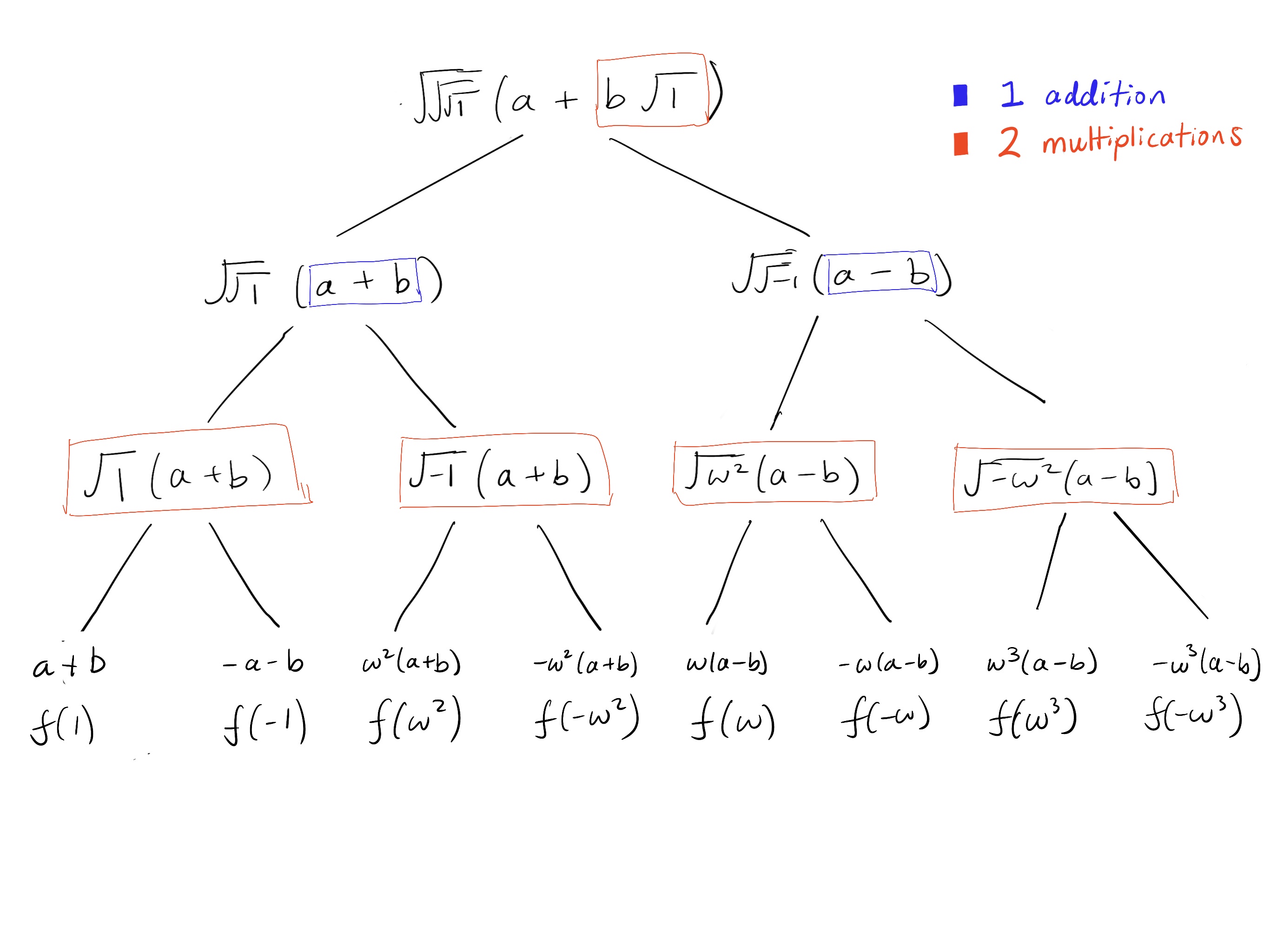
一种思考方式是

“在时钟上加两个数字 和 等同于乘以具有指数 和 的单位根，即 和 。”

如果我们取任何单位根并在指数上加 1，这等同于将该单位根乘以 （或仅 ）。例如，将 乘以 与在指数上加一得到 相同。

因此，将 -th 单位根乘以 或在指数上加 1，与围绕圆进行 -th 步相同。

例如，如果我们将 乘以 ，我们得到 ，这等于向前移动 1/4-th 步：

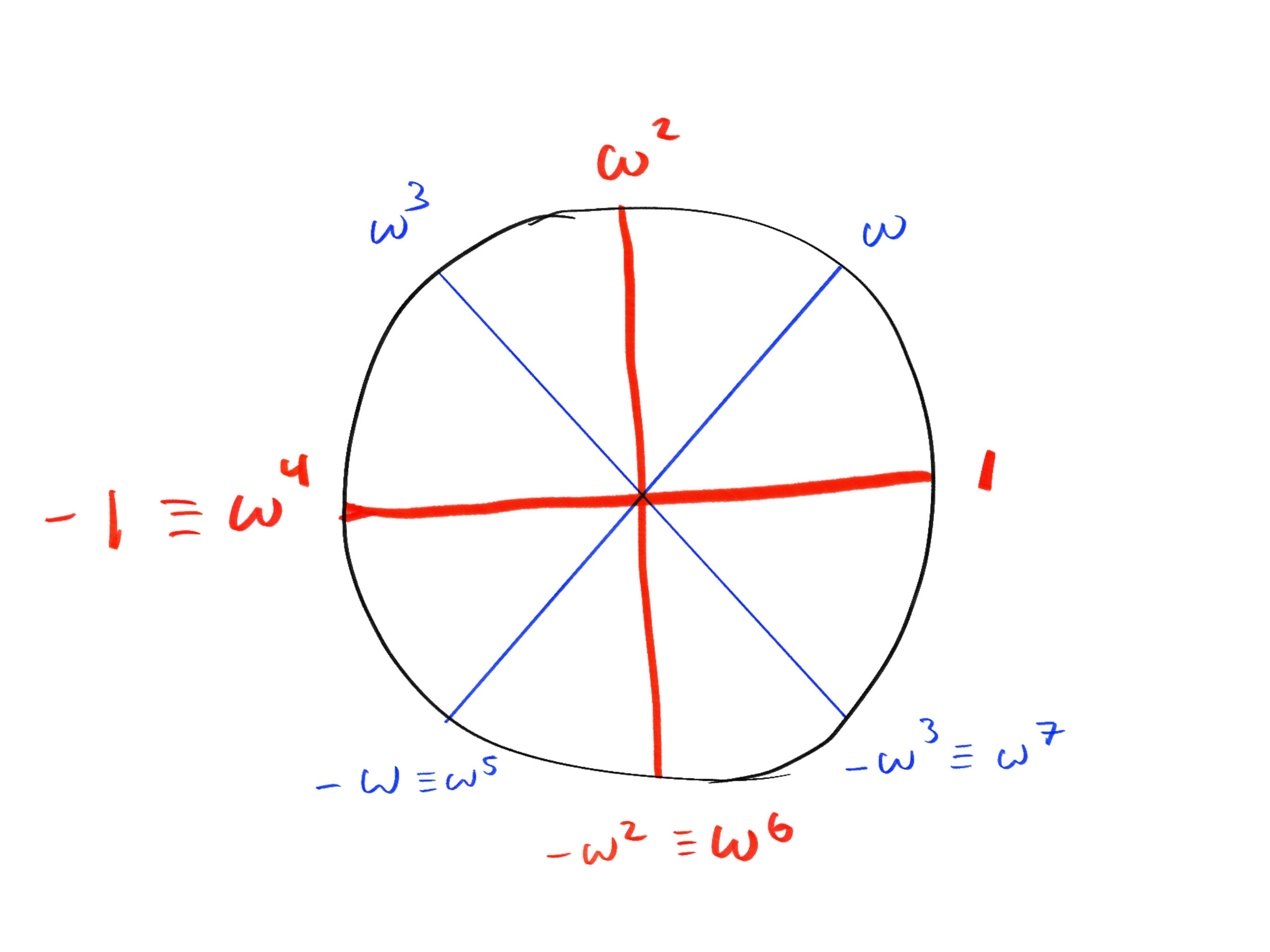
我们可以通过从 开始并重复在指数上加 1 来生成单位根，从而产生 ，依此类推，直到我们达到 ，此时结果将以模 环绕。这与围绕圆走 步完全相同。

使用单位圆可视化同余

让我们扩展这个圆以包括更多的同余。

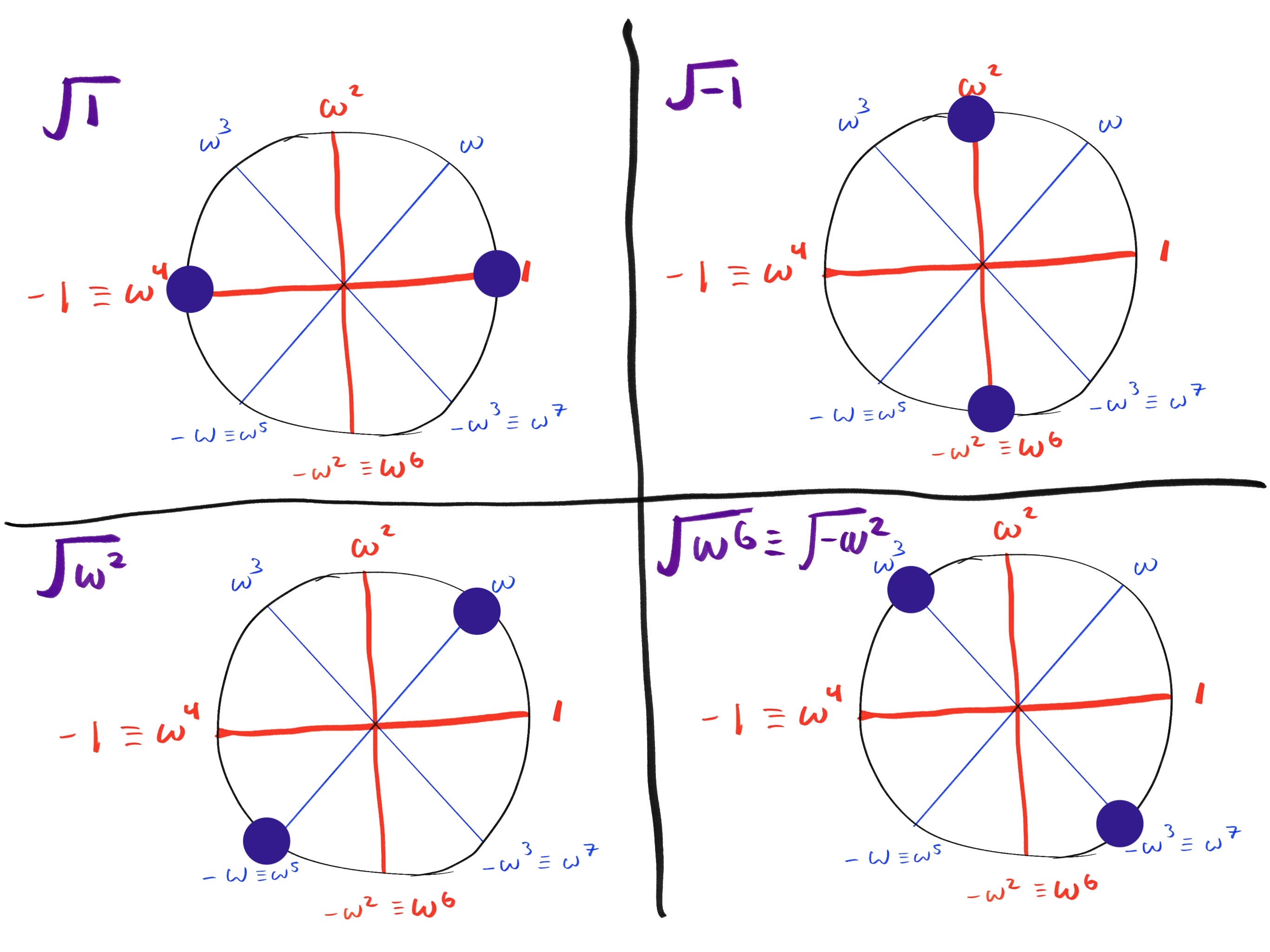
如果我们乘以 和 ，我们将得到 ，它与 同余，正如该图表所示：

另一种思考方式是从 开始并向前走 3 步：

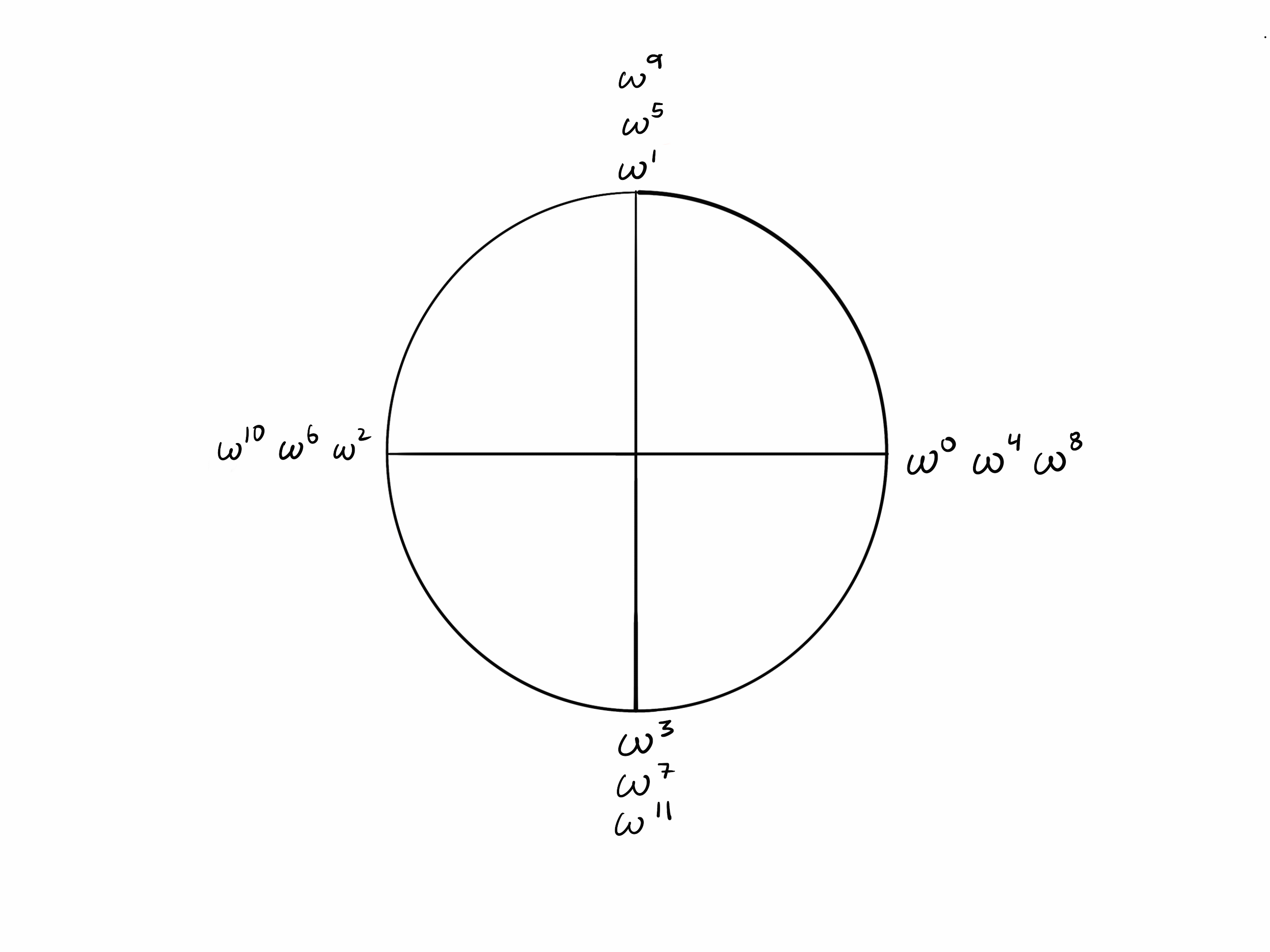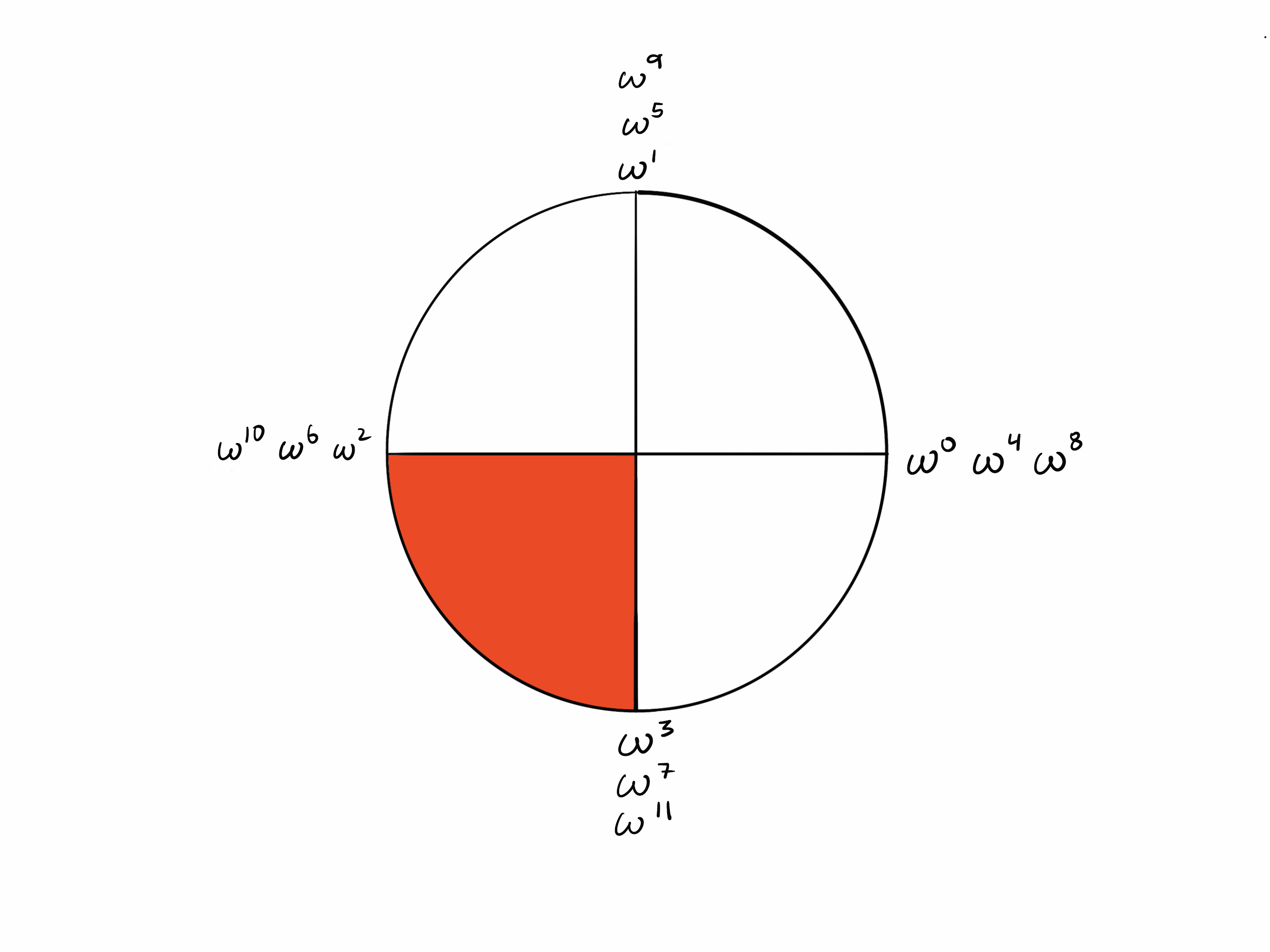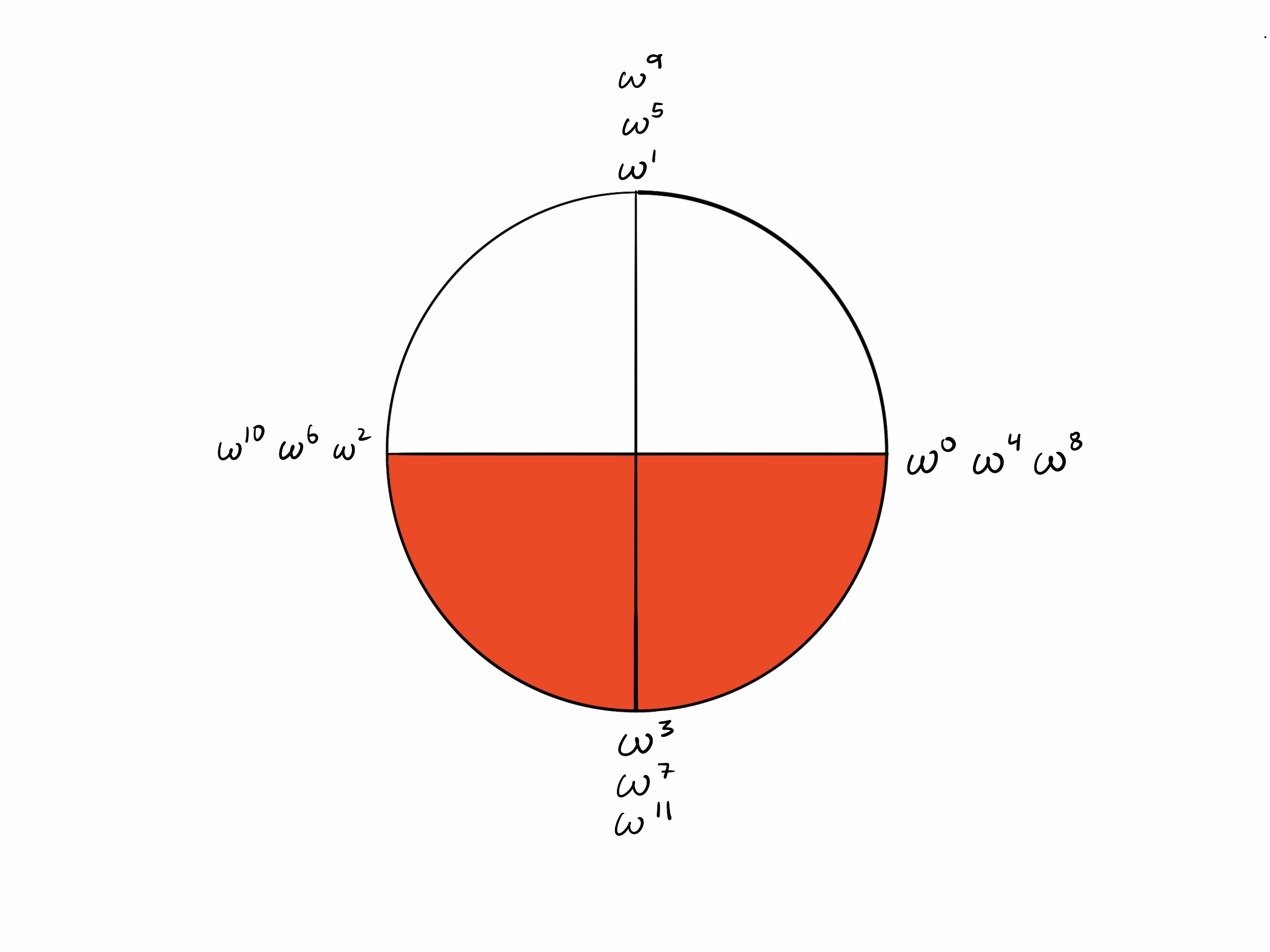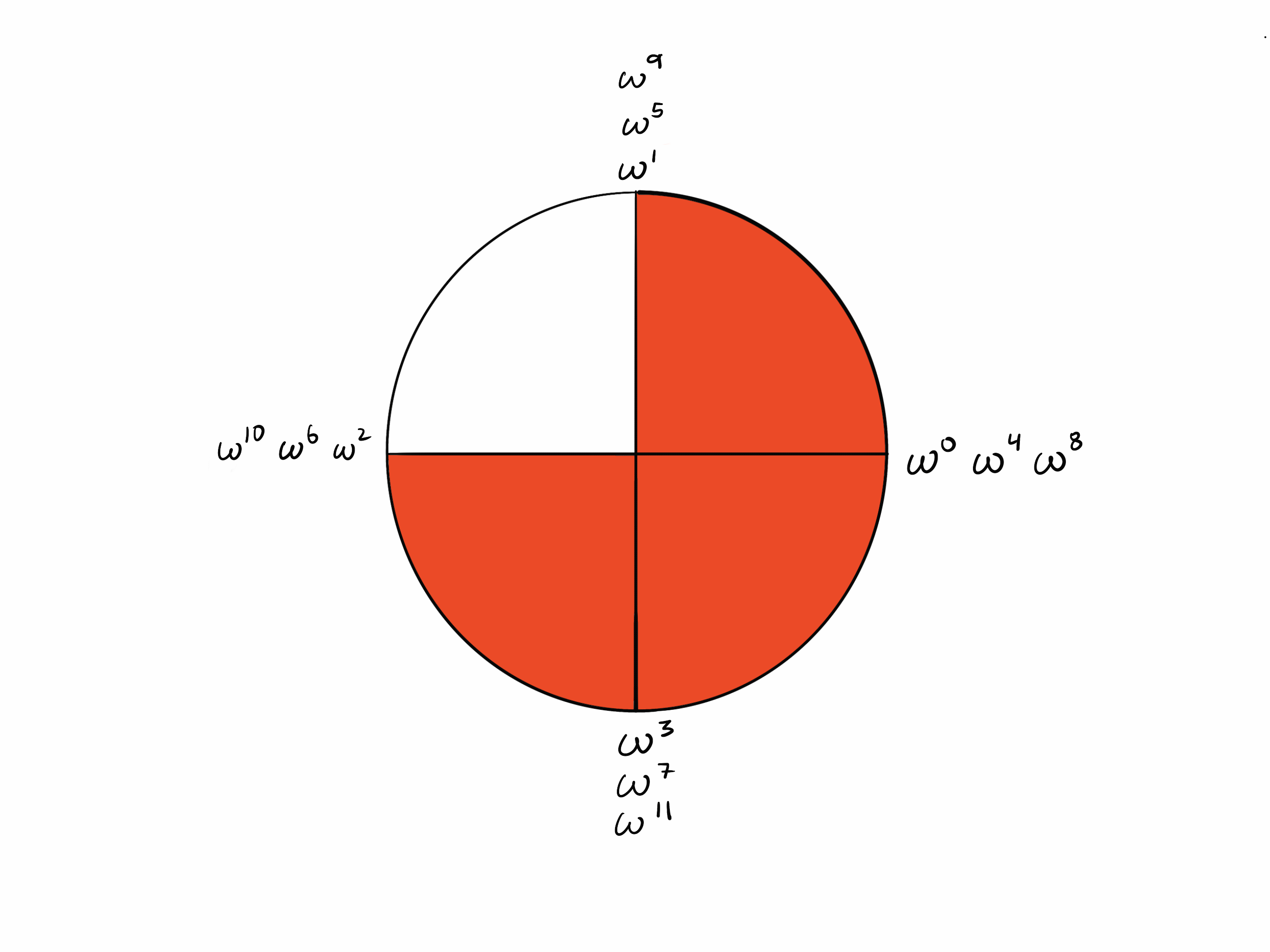
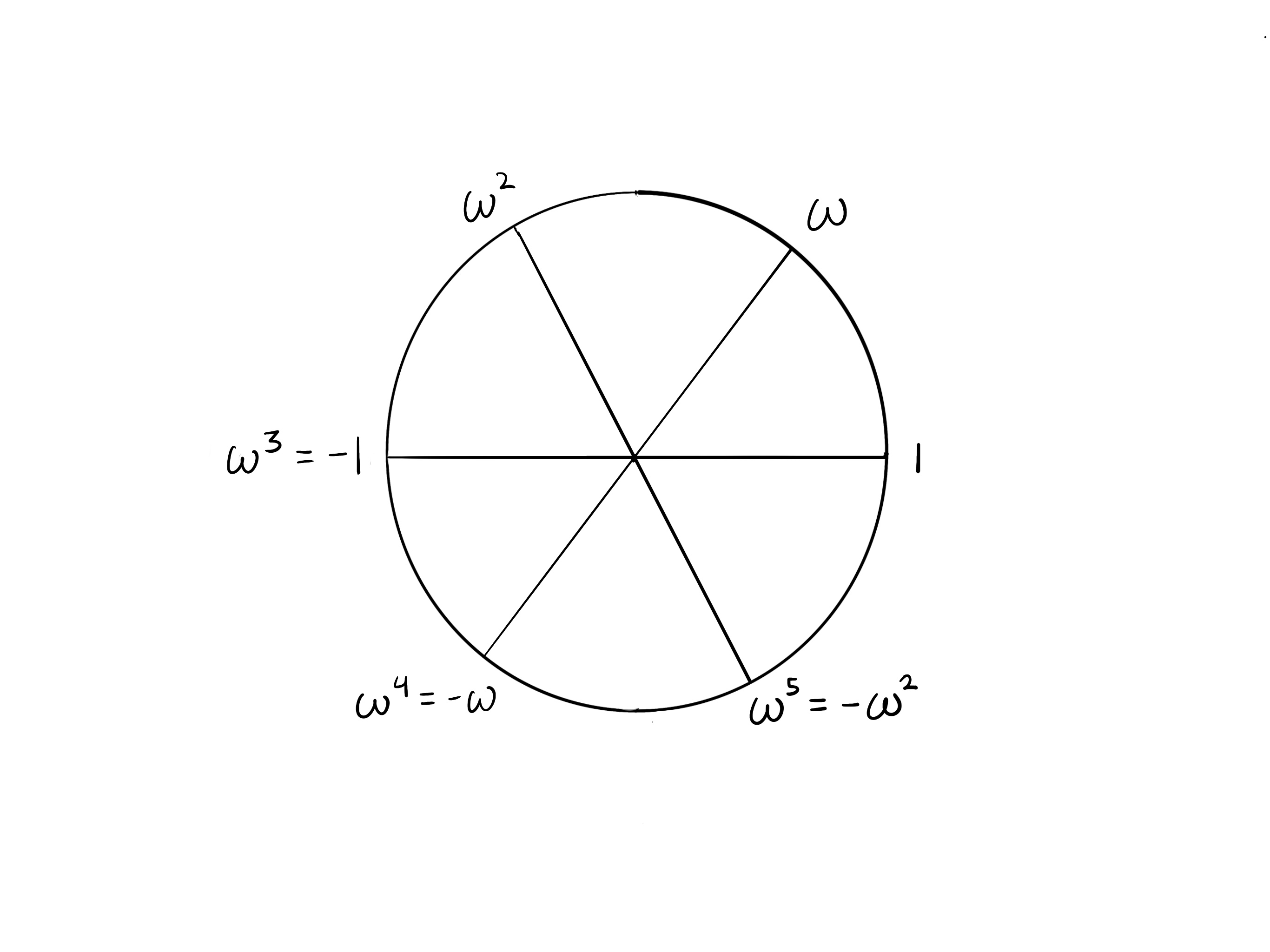
相距 k/2 步的点

由于需要 步才能“绕”圆， 步会将你从一个点带到对面的点。

现在观察 的圆中，对面的点是彼此的加法逆元（它们的和为零）。回想一下 。由于 k = 4，

在 的例子中，我们有

请注意，我们现在是加单位根在一起，而不是乘以它们，所以指数的加法规则不适用！不要将 与 混淆！单位根是有限域元素，并且域有 2 个运算：加法和乘法。

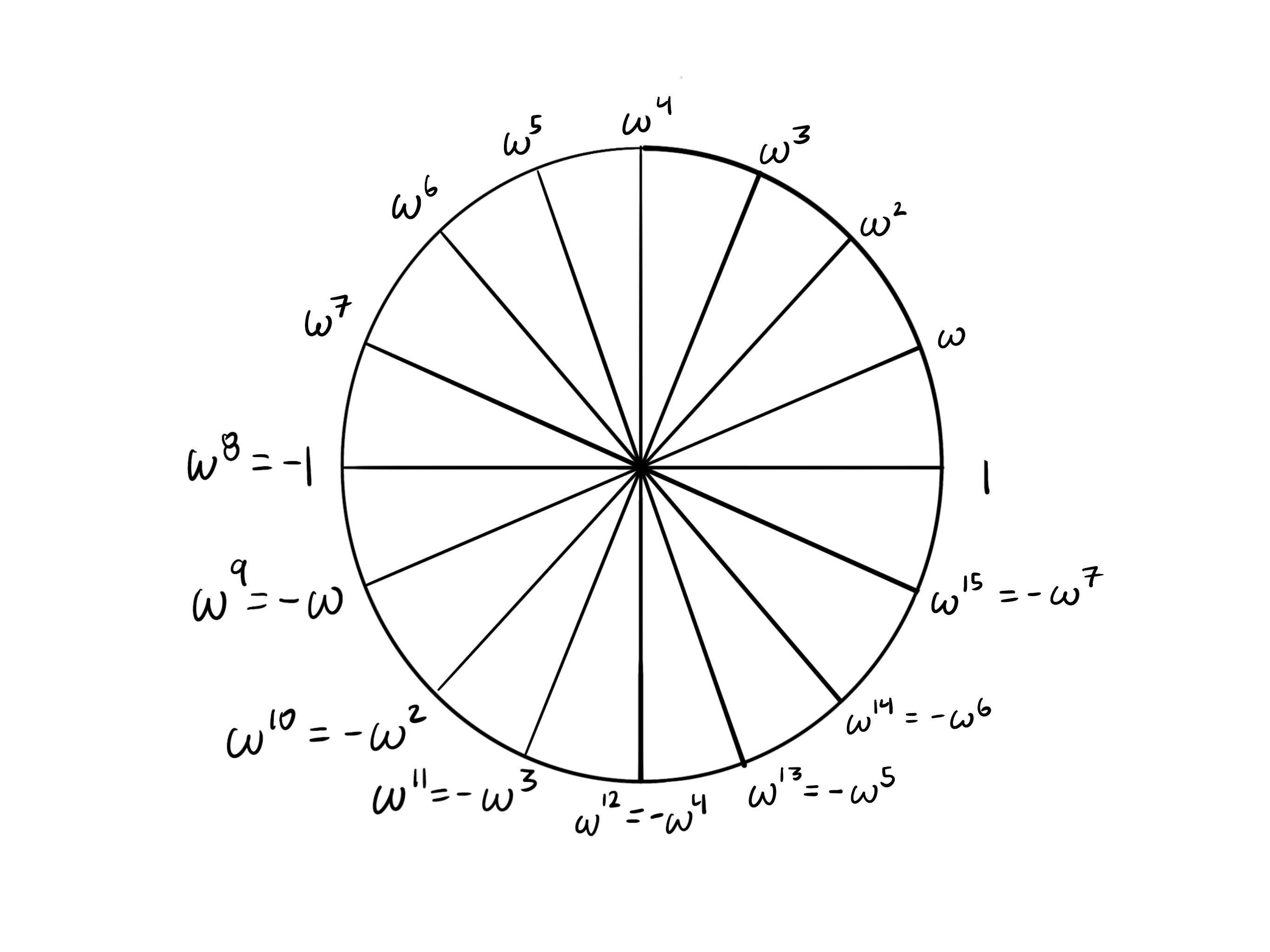
其他 k 值的示例

如果圆被划分为 段，那么采取 步会将你带到对立面。在每个显示的情况下，我们看到对立的点是加法逆元。

k = 8

k = 6

k = 16

总结

为了记住 是加法逆元（它们的和为零），我们画一个有 个点的圆，其中每一步都乘以 。对立的点将是加法逆元。

圆形图对于可视化单位根的子群以及平方根也非常有用——我们将在接下来的章节中展示这些可视化。

• 原文链接： rareskills.io/post/roots...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～