密码学基础：零知识证明（第一部分）

这是关于加密技术的系列文章的一部分。如果这是你遇到的第一篇文章，我强烈建议你从系列的开头开始阅读。

现在是时候讲解一些零知识证明了！

在这个系列的前面，我们概述了它们是什么。不过这次我们会更加深入地定义，并查看一个更高级的例子。

零知识证明（ZKP）的一般思想是说服某人某个关于一些信息的声明是真实的，而不泄露该信息。这一声明可能具有不同的性质。我们可能想证明：

• 知识某个离散对数（Schnorr 协议）
• 某个数字在某个范围内
• 一个元素是某个集合的成员

等等。通常，这些声明需要不同的证明系统，这意味着需要特定的协议。这在某种程度上是不实用的——如果我们能对知识证明进行概括，那将是非常好的。

所以我们的计划如下：我们将查看一种叫做Bulletproofs的ZKP技术。我们将看到它们如何解决一个非常特定的问题，并在接下来的几篇文章中评估几乎同样的事情如何以更一般的方式实现。

我们将专注于简单、未优化的版本（这已经足够复杂了！）。如果这篇文章不够满足你的好奇心，查看原始论文或这里的这篇文章可能就是你所寻找的。

在深入数学之前，让我们先简单介绍一下这个主题。

零知识基础

当我们谈论证明声明的有效性时，广义的技术家族称为知识证明（proofs of knowledge）。在这些类型的协议中，通常涉及两个参与者：一个证明者（prover）和一个验证者（verifier）。

还有两个关键要素：我们想要证明的声明，和一个见证（witness），这是一段信息，让我们能够有效地检查该声明是否为真。大概如下图所示：

但这并不是完整的故事！

如果你记得我们对Schnorr协议的简要回顾，我们看到证明者和验证者之间存在一些来回的通信。这是有充分理由的：验证者向证明者提供了一段不可预测的信息。这样做可以使得生成虚假证明极其困难——只要证明者是诚实的，产生有效证明就非常简单。这种“通配符”因素通常被称为挑战（challenge）。

一个简单的例子

为了理解这个想法，这里有一个很简单的练习：想象一下，Alice（Alice）将一组秘密的扑克牌面朝下放在桌子上。坐在桌子对面的Bob（Bob）想检查Alice是否知道这组秘密牌。他可以怎么做？

好吧，他可以问“告诉我第四张牌是什么”。如果Alice确实知道这组牌，她可以自信地回答“黑桃7”，而Bob可以仅仅查看那张面朝下的牌并检查其是否一致。Bob选择了一张牌提出了一个挑战，而只有通过对牌序列的诚实知识，Alice才能提供正确的信息。否则，她只能猜测——而她说对的牌的可能性是不太可能的。

当然，这不是零知识，因为序列的部分信息被揭示了！

将这个挑战加入到混合中，我们得到了一个更完整的图像：

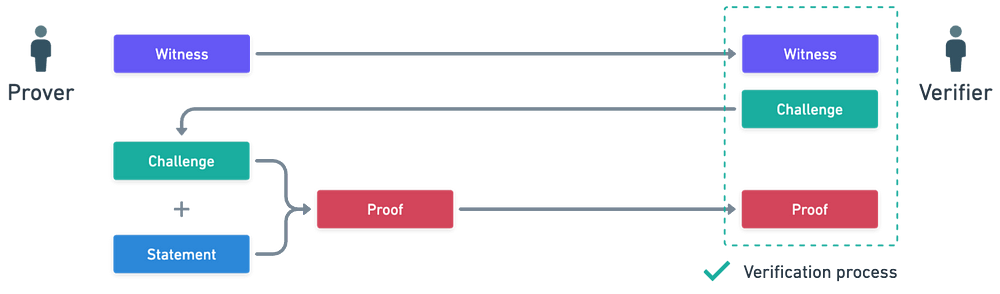
这个想法是，证明者在知道验证者的输入之前对他们的信息进行承诺，而在我们的例子中，Alice是通过将牌面朝下放置来承诺——这种做法在一定程度上防止了她作弊。

正式地说，我们刚刚描述的结构典型于西格玛协议。你可能还会见到公共币验证者这一术语，这意味着验证者的随机选择被公开。为了避免混淆，了解一下就好！

为了结束我们的简要介绍，这里是知识证明应该可以满足的两个关键属性：

• 完整性：一个诚实的证明者有诚实的声明，能够说服验证者该声明的有效性。
• 健壮性：一个拥有虚假声明的证明者不应该能够说服验证者该声明为真。或者说，这种情况发生的概率应该非常低。

现在，如果我们添加条件，使得证明不泄露关于声明的任何信息，那么我们就有了一个零知识证明。我们将不会正式定义“揭示什么都没有”是什么意思，但如果你想深入研究，有一些资源解释这一想法。

至此，介绍结束。前方有动荡，请保持镇定。

范围证明

如前所述，我们需要决定的是我们想证明什么。例如，在Schnorr协议的情况下，我们希望证明某个值的离散对数的知识。

我们更希望证明的另一个声明是某个值位于一个范围内。这在私人余额的系统中可能很有用，在此情况下，证明某个交易完成后，剩余余额是非负的（正数或零）就显得很重要。在这种情况下，我们只需证明该值位于一个范围内：

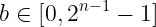
这就是Bulletproofs等技术发挥作用的地方。现在……我们到底如何证明这一点呢？

嗯……

切换视角

想象一个以字节（8位）表示的数字v。那么，这个数字的范围只能在0到255（2⁸ - 1）之间。因此，如果我们能够证明以下声明：

存在有效的8位表示v

那么我们就构建了一种知识证明，证明v位于0到255之间。就这样。

147的二进制表示，只需8位即可！

然而，我们必须将这个想法转化为一组数学约束，以表示我们的声明。

首先，让我们用aₗ₀, aₗ₁, aₗ₂, …表示v的位值——其中aₗ₀是最低有效位。这意味着以下等式成立：

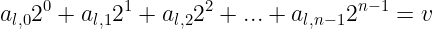
为了避免繁琐的表达，令我们引入一些新符号。...