加密学基础：安全性评估

这是有关加密技术的更大系列文章的一部分。如果这是你遇到的第一篇文章，我强烈建议从该系列的开头开始阅读。

在我们的旅程中，我们的目标始终是尝试理解现代加密学所基于的数学基础。这本身就是一个重要的考验——毕竟，加密学是关于构建极其困难的谜题。如果我们无法理解所涉及的工具，就无法进行构建。

尽管我们在设计加密协议的方式上仍有许多需要探索的内容，但我认为现在是时候稍作旁逸斜出，将注意力转向我们尚未讨论的一个方面。让我们尝试回答以下问题：

我们迄今为止所学的方法安全性如何？

我们到底理解什么是安全？

它是如何衡量的？

在我看来，回答这个问题的最佳方式是迅速回顾一下加密学的历史。通过这样做，我们将会遇到一些可能会从一开始就危及我们方法有效性的问题，而其他问题会逐渐变得明确。

那么让我们开始回顾最开始的部分。

凯撒密码

在通信中保护数据的想法肯定不是一个新鲜事物。

历史上有尝试在古代文明中隐藏秘密信息的记录。其中一个著名的例子，也是使用加密技巧的第一个记录案例，是凯撒密码（Caesar cipher），它可以追溯到公元前100年。这是一种非常简单的技术：字母表中的每个字母都被移动一定数量的位置。因此，这被归类为替代密码（substitution cipher），因为每个字母都按照一套特定的规则被替换为另一个字母。

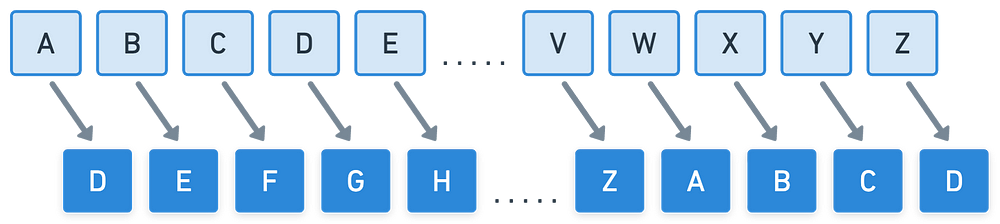
原始字符通过移动映射到新的字符

只要你知道字符移动了多少个位置，就可以解密使用这种技术加密的信息。例如，如果移动了 +3 个字母（如上图所示），那么密文“khooraruog”可以映射回原始文本“helloworld”。当然我们可以添加特定字符，但我们先保持最原始的简单方法。

一切都很好，直到有一个名叫 Al-Kindi 的人出现，并且破解了这个密码，利用了一个致命的缺陷。你能猜到是什么吗？

公正地说，差不多过去了近千年才有人提出这个利用方法，所以如果你没有想到这一点也不要太担心！

我把集体的失败算作个人的成功

破解

在任何语言中，一些字母的出现频率高于其他字母。如果我们对大量文本进行频率分析，会出现一种分布。对于英语，这种分布大致如下所示：

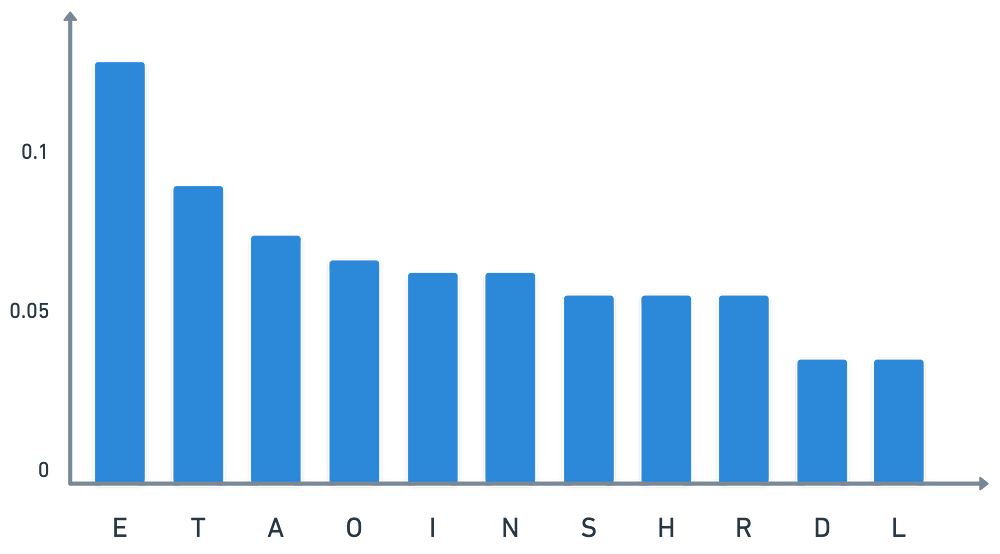
字母在英语文本中的出现频率

你问我们可以用这些信息做什么？好吧，如果消息恰好是一些英文文本，那么我们可以检查我们加密信息中字母的频率。而且，很可能出现频率最高的那个字母是字母E加密后的版本！

我们想一想：例如，如果字母E加密为字母P，那么可以推测P出现频率很高。这种情况发生的概率随着文本的长度增加而增加，因为字母开始重复。

这被称为频率分析（frequency analysis）。而这个问题真的只归结于和我们密文有关的非均匀分布。

我不记得之前是否提到过，不过密文是我们称之为加密过程输出的一种方式——而输入通常被称为明文。

因此，这意味着我们可以通过观察加密数据推断出一些信息。这是我们绝不应该能够做的。在“理想的”替代方法中，这意味着每个字符出现在密文中的概率是相等的，但是在凯撒密码中并非如此。

总之，这里传达的核心思想是：

我们不应该通过观察密文来了解加密数据中的任何信息。

而这正是我们迄今为止大多数技术引入某种类型的随机性的主要原因：使得事物在随机数据中变得不可区分。这意味着任何字符在密文中出现的几率几乎是一样的——换句话说，从概率角度来看，字符的分布是（接近于）均匀的：

密文字符的均匀概率分布

可以保证的是——如果这一条件未满足，则这种方法很可能不安全，因为这为基于密文分布的分析打开了大门。我们在设计加密方法时已经发现了一个安全要求。

密钥大小

安全性部分与缺乏这些后门或攻击向量有关，这些可能会危及我们保护数据努力的完整性，就像之前提到的例子一样。还有其他类型的攻击，例如选择明文攻击、侧信道攻击，等等。

仔细审查我们方法的每个方面是非常重要的，因为即便是最微小的漏洞都可能破坏整个系统。正如我在关于哈希的文章中提到过，现在重申：

一条链的强度仅取决于其最弱的一环。

但假设我们已经做好了功课，并且相当确信我们的技术非常牢固，没有明显的后门。那么我们还应担心什么？

暴力破解，就是这个！

是时候展示一些计算能力了

问题很简单：只凭借尝试与错误，破解一种加密方法会有多容易？我在之前的文章中简要提到过，但现在让我们试着量化这个任务。

简单来说，涉及此事的有两个要素：

• 底层数学结构的大小
• 解决我们问题所涉及操作的计算复杂性

例如，在椭圆曲线密码学（ECC）（Elliptic Curve Cryptography (ECC)）中，我们关心底层椭圆曲线组有多大，也关心逐个尝试值所需的计算努力。

RSA 密钥大小

不妨先不关注 ECC，让我们分析一下RSA。简单回顾一下：RSA 基于这样一个事实，即很难找到一个给定数字 n = p.q 的两个素因子。

我们先从小的开始。假设 p 和 q 最多为 1 字节（8 位）长。这意味着 n = p.q 最多为 2 字节长。找到其素因子的难度如何？

当然，这会是非常容易的。你可以自己尝试一下，写个快速脚本。为了让这个过程变得困难——因此对加密学有用——我们需要 p 和 q 大得多。随着我们使用更大的数字，因式分解变得指数级更难。

在 RSA 的早期，人们认为使用最大512位长的密钥（p 和 q）会使加密方案变得安全。但在过去几十年里，计算能力只增加，这使得解决512位密钥的因式分解问题在几天甚至几小时内就可能。听上去似乎不够安全…

那么该怎么办？增加密钥大小！因此，如今的推荐是使用2048位的密钥。据信，考虑到当前可用的计算能力，即使使用这些密钥大小，解决因式分解问题也需要一个非常非常长的时间。但随着计算机变得更强大，这一切可能会有所变化。

量子计算似乎就在不远的未来……所以谁知道呢！

ECC 密钥大小

相比之下，让我们看看使用椭圆曲线时会发生什么。我们提到过当乘以某个数字 m 时会涉及几步，这非常重要，因为每次我们尝试一个数字 m 并检查它是否解决了离散对数问题时都必须运行加倍加法算法：

这表明：暴力破解在计算上远比仅仅乘以两个数字（如 RSA 的情况）要更耗费用力——我们的底层结构更为复杂。这同时意味着我们可以通过更小的密钥大小实现相同程度的安全性。例如，256位的ECC密钥的安全性大约相当于3072位的RSA密钥。

密钥大小重要吗？

啊，这个问题很好！这里有几个因素需要考虑。

一般来说，密钥越大，计算成本就越高。计算[10]G和[1829788476189461]G的难度是不同的，对吧？因此，尽管我们知道增加密钥大小对安全性有好处，但这对速度绝对没有好处。所以，较大的密钥大小不总是更好。

为了避免误解，这里我们讨论的是密钥大小

选择正确的密钥大小实际上是一种权衡。这取决于我们最看重什么：速度、安全性，还是两者之间的折中。

如果我们对速度不太在意，并且需要我们的方法非常安全，那么就需要更大的密钥。但如果我们需要更快的算法，缩小密钥大小可能是一个选择。

总结

这篇简短的文章快速回顾了一些与安全性相关的最重要方面。实际上，这种分析属于一个完整的分支：密码分析（cryptanalysis），它与加密学是类似的关系。称这篇文章为密码分析文章几乎是不合适的——更确切地说，它是有关该学科的一些思想的非常温和的介绍。

然而，有一点是清楚的：设计加密方法与理解如何破解它们同样重要。跳过这种分析将使我们面临创建一种有缺陷的系统的风险，这最终无法确保我们可能向客户提供的安全保证——这可不妙。

我故意省略了介绍安全参数的概念，以保持内容的简单性。你可能会在论文或技术讨论中看到这个概念，因此你可能想要阅读一下，作为对上述讨论的一些概念的概括。

通过这些，我们至少对我们方法中可能存在的一些弱点有了一个总体了解——虽然这方面还有很多内容需要覆盖。请始终记住，安全性并不与数学的复杂性挂钩。复杂的并不等于安全，仔细的分析始终是良好的实践！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～