椭圆曲线密码学中的阶和子群阶

ECC 中的阶和子群阶

所以，中本聪选择了 secp256k1 曲线，剩下的就是历史了。但是，一条曲线是如何设计的呢？嗯，在 ECC 中，我们可以有一个方程 y²=x³+ax+b (mod p)。对于 a=2, b=3 和 p=97，我们得到可能的点 [ 这里]:

(1,54) (1,43) (3,91) (3,6) (4,47) (4,50) (10,76) (10,21) (11,17) (11,80)
(12,94) (12,3) (17,87) (17,10) (20,34) (20,63) (21,73) (21,24) (22,92)
(22,5) (23,73) (23,24) (24,95) (24,2) (25,35) (25,62) (27,7) (27,90) (28,34)
(28,63) (29,54) (29,43) (32,7) (32,90) (37,22) (37,75) (38,7) (38,90) (39,91)
(39,6) (44,77) (44,20) (46,72) (46,25) (47,79) (47,18) (49,34) (49,63) (50,19) (50,78) (52,68) (52,29) (53,73) (53,24) (54,85) (54,12) (55,91) (55,6) (56,89) (56,8) (59,65) (59,32) (65,65) (65,32) (67,54) (67,43) (70,65) (70,32) (73,83) (73,14) (74,77) (74,20) (76,77) (76,20) (80,87) (80,10) (83,74) (83,23) (84,37) (84,60) (85,26) (85,71) (86,69) (86,28) (87,27) (87,70) (88,41) (88,56) (91,39) (91,58) (92,81) (92,16) (95,66) (95,31) (97,87) (97,10)

你可以用 (1,54) 来检验，因为 54² (mod 97) 是 6, 并且 1³+2 x 1 + 3 (mod 97) 也是 6。对于 (3,91)，我们有 91² (mod 97) 是 36, 并且 3³+ 2 x 3 + 3 (mod 97) 是 36。 对于 x=2, 和 x=5，没有解。一个基本的图是 [ 这里]:

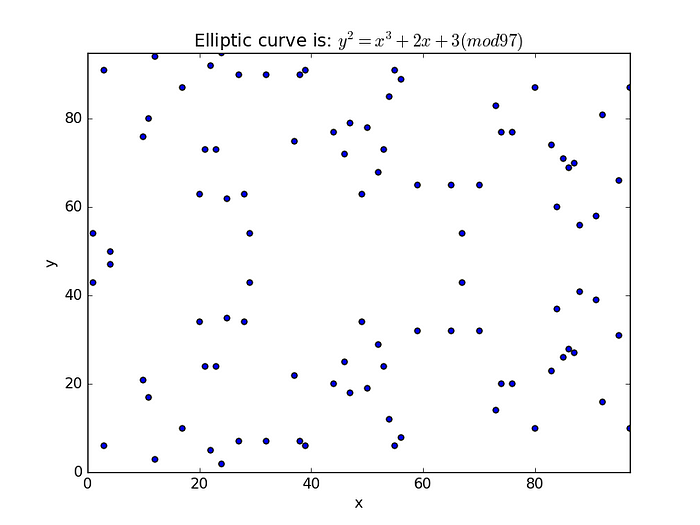
对于公钥加密，我们必须创建一个基点 (G)，然后将其加 n 次（以获得 nG）。 nG 的值将是我们的公钥，n 的值将是我们的私钥。因此，让我们使用 Sage 来确定可能的点的总数（基数）：

a = 2
b = 3
p = 97
E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())
card = E.cardinality()
print("cardinality =",card)

这给出：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100

这意味着我们有 100 个点构成曲线的群——这个值被称为群的阶。某些曲线包含群中的所有点，但其他曲线具有子群，其中每个群中的点数较少。

在此范围内，可以有许多循环子群。 为了找到这些，我们确定阶的素因子，我们确定：

n = h x r

并且，其中 h 是子群的数量（也称为 cofactor），r 是每个子群中的点数。 保持 EC 点的子群的数量 h 称为 cofactor。 对于 secp256k1，我们的 cofactor 为 1，这意味着所有点都在群中，没有子群。 对于 Curve 25519，我们的 cofactor 为 8，，对于 Curve 448， cofactor 为 4。

100= 2x2x5x

因此，我们具有循环子群 2、5、25 和 50。 让我们尝试 (3,91) 的基点 [ 这里]:

a= 2
b= 3
p= 97
n= 18
x-point= 3
P (3,91) Point is on curve  # P (3,91) 点在曲线上
2P (80,87) Point is on curve # 2P (80,87) 点在曲线上
3P (80,10) Point is on curve # 3P (80,10) 点在曲线上
4P (3,6) Point is on curve  # 4P (3,6) 点在曲线上
5P=0
6P (3,91) Point is on curve  # 6P (3,91) 点在曲线上
7P (80,87) Point is on curve # 7P (80,87) 点在曲线上
8P (80,10) Point is on curve # 8P (80,10) 点在曲线上
9P (3,6) Point is on curve  # 9P (3,6) 点在曲线上
10P=0
11P (3,91) Point is on curve # 11P (3,91) 点在曲线上
12P (80,87) Point is on curve# 12P (80,87) 点在曲线上
13P (80,10) Point is on curve# 13P (80,10) 点在曲线上
14P (3,6) Point is on curve # 14P (3,6) 点在曲线上
15P=0
16P (3,91) Point is on curve# 16P (3,91) 点在曲线上
17P (80,87) Point is on curve# 17P (80,87) 点在曲线上
18P (80,10) Point is on curve# 18P (80,10) 点在曲线上

我们将此点的阶 (N) 定义为 N=5。 我们将其定义为由 P 生成的子组具有 5 个点。 我们可以使用 Sage 检查：

b = 3
p = 97

E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())

card = E.cardinality()
print("cardinality =",card)
factor(card)

G = E(3,91)
print("Generator order q=", G.order()) #打印生成器阶 q=

结果是：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100
Generator order q= 5

现在让我们尝试 (1,54) 的基点 [ 这里]:

a= 2
b= 3
p= 97
n= 18
x-point= 1
P (1,54) Point is on curve  # P (1,54) 点在曲线上
2P (92,81) Point is on curve # 2P (92,81) 点在曲线上
3P (0,87) Point is on curve  # 3P (0,87) 点在曲线上
4P (21,24) Point is on curve # 4P (21,24) 点在曲线上
5P (53,24) Point is on curve # 5P (53,24) 点在曲线上
6P (65,65) Point is on curve # 6P (65,65) 点在曲线上
7P (85,71) Point is on curve # 7P (85,71) 点在曲线上
8P (46,72) Point is on curve # 8P (46,72) 点在曲线上
9P (23,73) Point is on curve # 9P (23,73) 点在曲线上
10P (3,6) Point is on curve  # 10P (3,6) 点在曲线上
11P (87,70) Point is on curve # 11P (87,70) 点在曲线上
12P (52,29) Point is on curve# 12P (52,29) 点在曲线上
13P (47,18) Point is on curve# 13P (47,18) 点在曲线上
14P (74,20) Point is on curve# 14P (74,20) 点在曲线上
15P (88,41) Point is on curve# 15P (88,41) 点在曲线上
16P (32,90) Point is on curve# 16P (32,90) 点在曲线上
17P (17,87) Point is on curve# 17P (17,87) 点在曲线上
18P (95,31) Point is on curve# 18P (95,31) 点在曲线上

我们可以看到，（1,54）是一个更好的基点，因为它在我们选择的 n 值范围内不会循环。 事实上，在这种情况下，由 P 生成的子群有 50 个点。

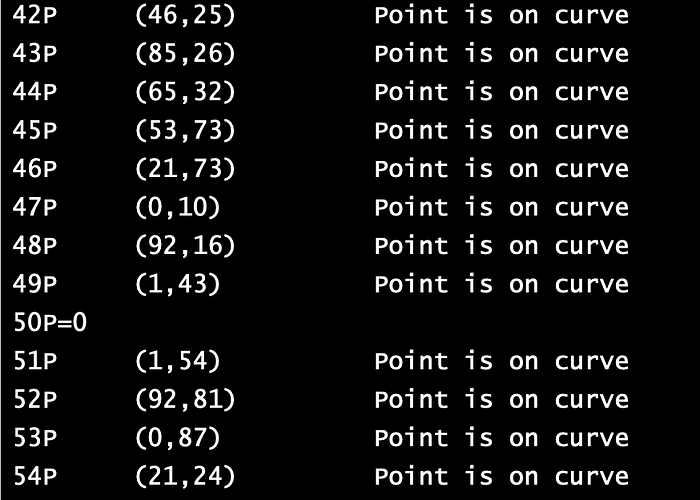
我们可以再次使用 Sage 进行计算：

a = 2
b = 3
p = 97
E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())
card = E.cardinality()
print("cardinality =",card)
factor(card)
G = E(1,54)
print("Generator order q=", G.order()) # 打印生成器阶 q=

这给出：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100
Generator order q= 50

我们在这里看到子群的阶是 50。对于 (21,73) 的基点，我们得到：

a= 2
b= 3
p= 97
n= 80
x-point= 21
P (21,73)    Point is on curve # P (21,73) 点在曲线上
2P (46,25)    Point is on curve # 2P (46,25) 点在曲线上
3P (52,68)    Point is on curve # 3P (52,68) 点在曲线上
4P (32,7)    Point is on curve  # 4P (32,7) 点在曲线上
5P (80,87)    Point is on curve # 5P (80,87) 点在曲线上
6P (84,37)    Point is on curve # 6P (84,37) 点在曲线上
7P (24,95)    Point is on curve # 7P (24,95) 点在曲线上
8P (95,31)    Point is on curve # 8P (95,31) 点在曲线上
9P (74,20)    Point is on curve # 9P (74,20) 点在曲线上
10P (3,6)    Point is on curve  # 10P (3,6) 点在曲线上
11P (65,65)    Point is on curve# 11P (65,65) 点在曲线上
12P (92,81)    Point is on curve# 12P (92,81) 点在曲线上
13P (92,16)    Point is on curve# 13P (92,16) 点在曲线上
14P (65,32)    Point is on curve# 14P (65,32) 点在曲线上
15P (3,91)    Point is on curve # 15P (3,91) 点在曲线上
16P (74,77)    Point is on curve# 16P (74,77) 点在曲线上
17P (95,66)    Point is on curve# 17P (95,66) 点在曲线上
18P (24,2)    Point is on curve  # 18P (24,2) 点在曲线上
19P (84,60)    Point is on curve# 19P (84,60) 点在曲线上
20P (80,10)    Point is on curve# 20P (80,10) 点在曲线上
21P (32,90)    Point is on curve# 21P (32,90) 点在曲线上
22P (52,29)    Point is on curve# 22P (52,29) 点在曲线上
23P (46,72)    Point is on curve# 23P (46,72) 点在曲线上
24P (21,24)    Point is on curve# 24P (21,24) 点在曲线上
25P=0
26P (21,73)    Point is on curve# 26P (21,73) 点在曲线上
27P (46,25)    Point is on curve# 27P (46,25) 点在曲线上
28P (52,68)    Point is on curve# 28P (52,68) 点在曲线上

它的子群阶为 25。 如果我们尝试：

a = 2
b = 3
p = 97

E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())

card = E.cardinality()
print("cardinality =",card)
factor(card)

G = E(21,73)
print("Generator order q=", G.order()) # 打印生成器阶 q=

我们现在得到一个子群阶 25：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100
Generator order q= 25

对于 (88,41) 的基点，我们得到：

a= 2
b= 3
p= 97
n= 80
x-point= 88
P (88,41)    Point is on curve # P (88,41) 点在曲线上
2P (80,87)    Point is on curve # 2P (80,87) 点在曲线上
3P (53,73)    Point is on curve # 3P (53,73) 点在曲线上
4P (3,6)    Point is on curve  # 4P (3,6) 点在曲线上
5P (30,0)    Point is on curve # 5P (30,0) 点在曲线上
6P (3,91)    Point is on curve # 6P (3,91) 点在曲线上
7P (53,24)    Point is on curve # 7P (53,24) 点在曲线上
8P (80,10)    Point is on curve # 8P (80,10) 点在曲线上
9P (88,56)    Point is on curve # 9P (88,56) 点在曲线上
10P=0
11P (88,41)    Point is on curve# 11P (88,41) 点在曲线上
12P (80,87)    Point is on curve# 12P (80,87) 点在曲线上
13P (53,73)    Point is on curve# 13P (53,73) 点在曲线上
14P (3,6)    Point is on curve  # 14P (3,6) 点在曲线上
15P (30,0)    Point is on curve# 15P (30,0) 点在曲线上
16P (3,91)    Point is on curve# 16P (3,91) 点在曲线上
17P (53,24)    Point is on curve# 17P (53,24) 点在曲线上
18P (80,10)    Point is on curve# 18P (80,10) 点在曲线上
19P (88,56)    Point is on curve# 19P (88,56) 点在曲线上

并使用 Sage 检查：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100
Generator order q= 10

然后我们可以看到 挑选基点会对我们拥有的子群的大小产生重大影响。 现在让我们创建一个 Sage 程序来确定群，以及给定基点的每个子群的大小：

a = 2
b = 3
p = 97

E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())

card = E.cardinality()
print("cardinality =",card)
factor(card)

pts=E.points()
print("Points: ",pts) # 打印点：

for i in range(0,p):
 try:
  p=pts[i]
  G=E(p[0],p[1])
  print(f"({p[0]},{p[1]}). Generator order q=", G.order()) # 打印生成器阶 q=
 except:
  continue

当我们运行时，得到：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100
Points:  [(0 : 1 : 0), (0 : 10 : 1), (0 : 87 : 1), (1 : 43 : 1), (1 : 54 : 1), (3 : 6 : 1), (3 : 91 : 1), (4 : 47 : 1), (4 : 50 : 1), (10 : 21 : 1), (10 : 76 : 1), (11 : 17 : 1), (11 : 80 : 1), (12 : 3 : 1), (12 : 94 : 1), (17 : 10 : 1), (17 : 87 : 1), (20 : 34 : 1), (20 : 63 : 1), (21 : 24 : 1), (21 : 73 : 1), (22 : 5 : 1), (22 : 92 : 1), (23 : 24 : 1), (23 : 73 : 1), (24 : 2 : 1), (24 : 95 : 1), (25 : 35 : 1), (25 : 62 : 1), (27 : 7 : 1), (27 : 90 : 1), (28 : 34 : 1), (28 : 63 : 1), (29 : 43 : 1), (29 : 54 : 1), (30 : 0 : 1), (32 : 7 : 1), (32 : 90 : 1), (37 : 22 : 1), (37 : 75 : 1), (38 : 7 : 1), (38 : 90 : 1), (39 : 6 : 1), (39 : 91 : 1), (44 : 20 : 1), (44 : 77 : 1), (46 : 25 : 1), (46 : 72 : 1), (47 : 18 : 1), (47 : 79 : 1), (49 : 34 : 1), (49 : 63 : 1), (50 : 19 : 1), (50 : 78 : 1), (52 : 29 : 1), (52 : 68 : 1), (53 : 24 : 1), (53 : 73 : 1), (54 : 12 : 1), (54 : 85 : 1), (55 : 6 : 1), (55 : 91 : 1), (56 : 8 : 1), (56 : 89 : 1), (59 : 32 : 1), (59 : 65 : 1), (65 : 32 : 1), (65 : 65 : 1), (67 : 43 : 1), (67 : 54 : 1), (68 : 0 : 1), (70 : 32 : 1), (70 : 65 : 1), (73 : 14 : 1), (73 : 83 : 1), (74 : 20 : 1), (74 : 77 : 1), (76 : 20 : 1), (76 : 77 : 1), (80 : 10 : 1), (80 : 87 : 1), (83 : 23 : 1), (83 : 74 : 1), (84 : 37 : 1), (84 : 60 : 1), (85 : 26 : 1), (85 : 71 : 1), (86 : 28 : 1), (86 : 69 : 1), (87 : 27 : 1), (87 : 70 : 1), (88 : 41 : 1), (88 : 56 : 1), (91 : 39 : 1), (91 : 58 : 1), (92 : 16 : 1), (92 : 81 : 1), (95 : 31 : 1), (95 : 66 : 1), (96 : 0 : 1)]
(0,10). Generator order q= 50 # (0,10). 生成器阶 q= 50
(0,87). Generator order q= 50 # (0,87). 生成器阶 q= 50
(1,43). Generator order q= 50 # (1,43). 生成器阶 q= 50
(1,54). Generator order q= 50 # (1,54). 生成器阶 q= 50
(3,6). Generator order q= 5   # (3,6). 生成器阶 q= 5
(3,91). Generator order q= 5  # (3,91). 生成器阶 q= 5
(4,47). Generator order q= 50 # (4,47). 生成器阶 q= 50
(4,50). Generator order q= 50 # (4,50). 生成器阶 q= 50
(10,21). Generator order q= 50# (10,21). 生成器阶 q= 50
(10,76). Generator order q= 50# (10,76). 生成器阶 q= 50
(11,17). Generator order q= 50# (11,17). 生成器阶 q= 50
(11,80). Generator order q= 50# (11,80). 生成器阶 q= 50
(12,3). Generator order q= 50 # (12,3). 生成器阶 q= 50
(12,94). Generator order q= 50# (12,94). 生成器阶 q= 50
(17,10). Generator order q= 50# (17,10). 生成器阶 q= 50
(17,87). Generator order q= 50# (17,87). 生成器阶 q= 50
(20,34). Generator order q= 50# (20,34). 生成器阶 q= 50
(20,63). Generator order q= 50# (20,63). 生成器阶 q= 50
(21,24). Generator order q= 25# (21,24). 生成器阶 q= 25
(21,73). Generator order q= 25# (21,73). 生成器阶 q= 25
(22,5). Generator order q= 50 # (22,5). 生成器阶 q= 50
(22,92). Generator order q= 50# (22,92). 生成器阶 q= 50
(23,24). Generator order q= 50# (23,24). 生成器阶 q= 50
(23,73). Generator order q= 50# (23,73). 生成器阶 q= 50
(24,2). Generator order q= 25  # (24,2). 生成器阶 q= 25
(24,95). Generator order q= 25# (24,95). 生成器阶 q= 25
(25,35). Generator order q= 50# (25,35). 生成器阶 q= 50
(25,62). Generator order q= 50# (25,62). 生成器阶 q= 50
(27,7). Generator order q= 50 # (27,7). 生成器阶 q= 50
(27,90). Generator order q= 50# (27,90). 生成器阶 q= 50
(28,34). Generator order q= 50# (28,34). 生成器阶 q= 50
(28,63). Generator order q= 50# (28,63). 生成器阶 q= 50
(29,43). Generator order q= 10# (29,43). 生成器阶 q= 10
(29,54). Generator order q= 10# (29,54). 生成器阶 q= 10
(30,0). Generator order q= 2  # (30,0). 生成器阶 q= 2
(32,7). Generator order q= 25  # (32,7). 生成器阶 q= 25
(32,90). Generator order q= 25# (32,90). 生成器阶 q= 25
(37,22). Generator order q= 50# (37,22). 生成器阶 q= 50
(37,75). Generator order q= 50# (37,75). 生成器阶 q= 50
(38,7). Generator order q= 50 # (38,7). 生成器阶 q= 50
(38,90). Generator order q= 50# (38,90). 生成器阶 q= 50
(39,6). Generator order q= 50 # (39,6). 生成器阶 q= 50
(39,91). Generator order q= 50# (39,91). 生成器阶 q= 50
(44,20). Generator order q= 10# (44,20). 生成器阶 q= 10
(44,77). Generator order q= 10# (44,77). 生成器阶 q= 10
(46,25). Generator order q= 25# (46,25). 生成器阶 q= 25
(46,72). Generator order q= 25# (46,72). 生成器阶 q= 25
(47,18). Generator order q= 50# (47,18). 生成器阶 q= 50
(47,79). Generator order q= 50# (47,79). 生成器阶 q= 50
(49,34). Generator order q= 50# (49,34). 生成器阶 q= 50
(49,63). Generator order q= 50# (49,63). 生成器阶 q= 50
(50,19). Generator order q= 50# (50,19). 生成器阶 q= 50
(50,78). Generator order q= 50# (50,78). 生成器阶 q= 50
(52,29). Generator order q= 25# (52,29). 生成器阶 q= 25
(52,68). Generator order q= 25# (52,68). 生成器阶 q= 25
(53,24). Generator order q= 10# (53,24). 生成器阶 q= 10
(53,73). Generator order q= 10# (53,73). 生成器阶 q= 10
(54,12). Generator order q= 50# (54,12). 生成器阶 q= 50
(54,85). Generator order q= 50# (54,85). 生成器阶 q= 50
(

>- 原文链接： [billatnapier.medium.com/...](https://billatnapier.medium.com/order-and-sub-oroups-orders-in-ecc-c818c0e7f133)
>- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～