使用平方根展开评估多值函数
- RareSkills
- 发布于 2025-11-12 11:32
- 阅读 2017
本文介绍了使用平方根展开方法在单位根上评估多值函数。通过将函数转换为多值函数并在域上进行评估,避免了直接在单位根上进行评估的复杂性。文章详细展示了如何通过嵌套平方根来展开和简化计算,并探讨了不同类型的项(如 和 )的计算复杂性,以及如何优化多项式以减少计算量,最终引出快速数论变换(NTT)算法。
在前一章关于多值函数的图像保持中,我们看到与其在单位根上计算 ,不如将 转换为一个多值函数并在域 上计算它。
展开平方根
将 1 的 8 次方根视为嵌套平方根要容易得多:
现在我们展示如何使用平方根展开来计算:
我们知道 等于 ,因此我们用它的计算结果替换最里面的 1 的平方根:
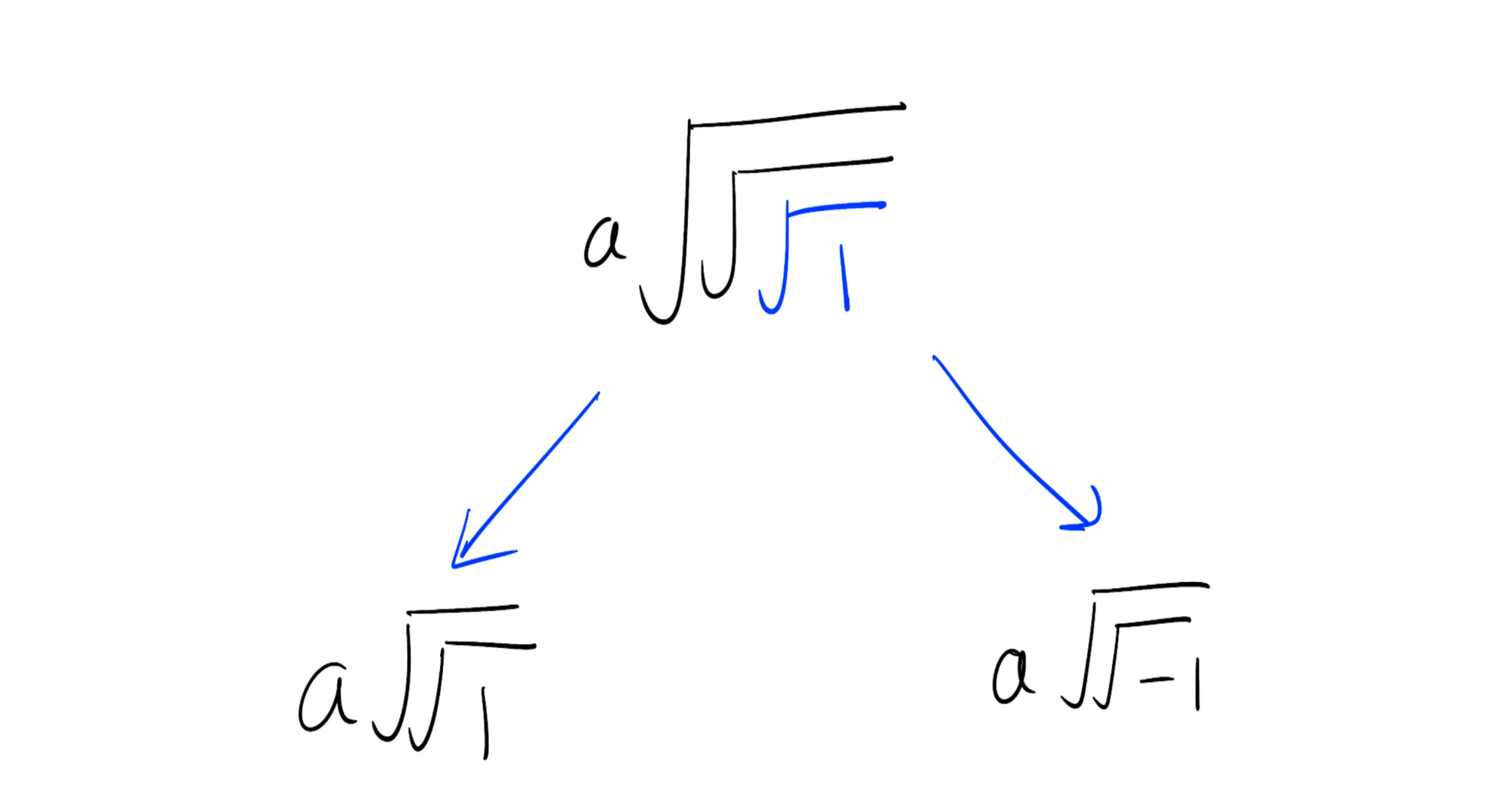
这“移除”了一层平方根。接下来,我们计算 和 。由于我们使用 1 的 8 次方根,所以
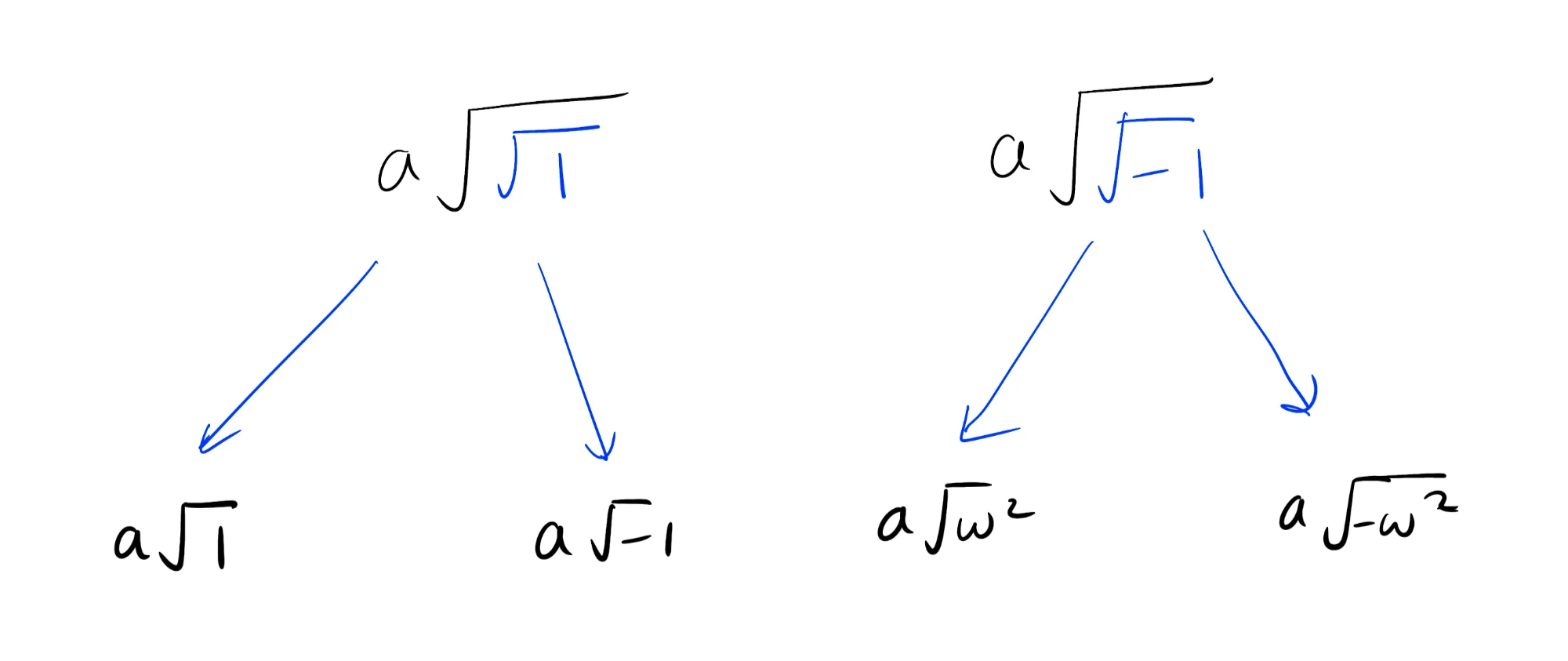
然后,我们计算剩余的每个平方根:
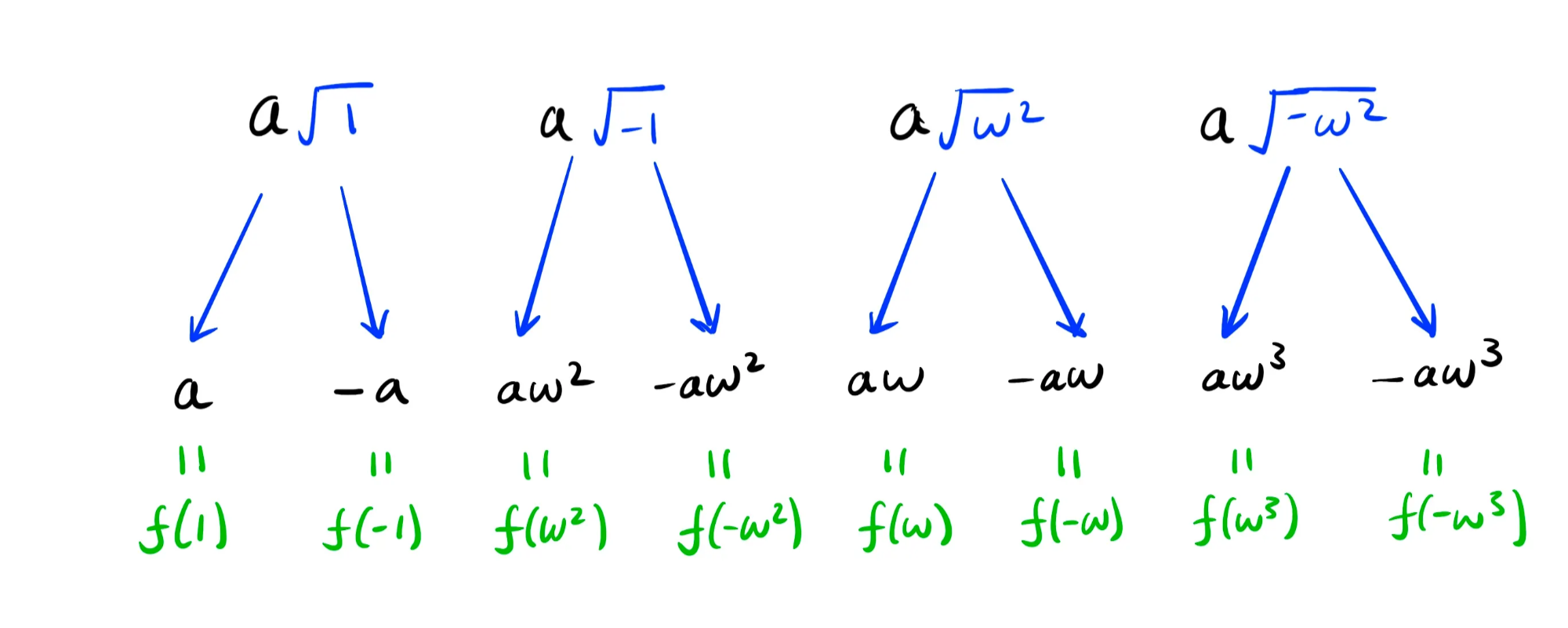
观察到,计算树的“叶子”完全是 在单位根上计算的 。
在 1 的 8 次方根上计算
平方根展开的好处在于,对于 的大多数次幂,平方根会“提前消失”,如下例所示。我们将 替换为 ,但由于 是平方,我们最终得到 或
这是通过重复展开平方根直到我们有八个计算结果的计算树。在最后一行,当没有平方根时,我们只需将值复制下来。
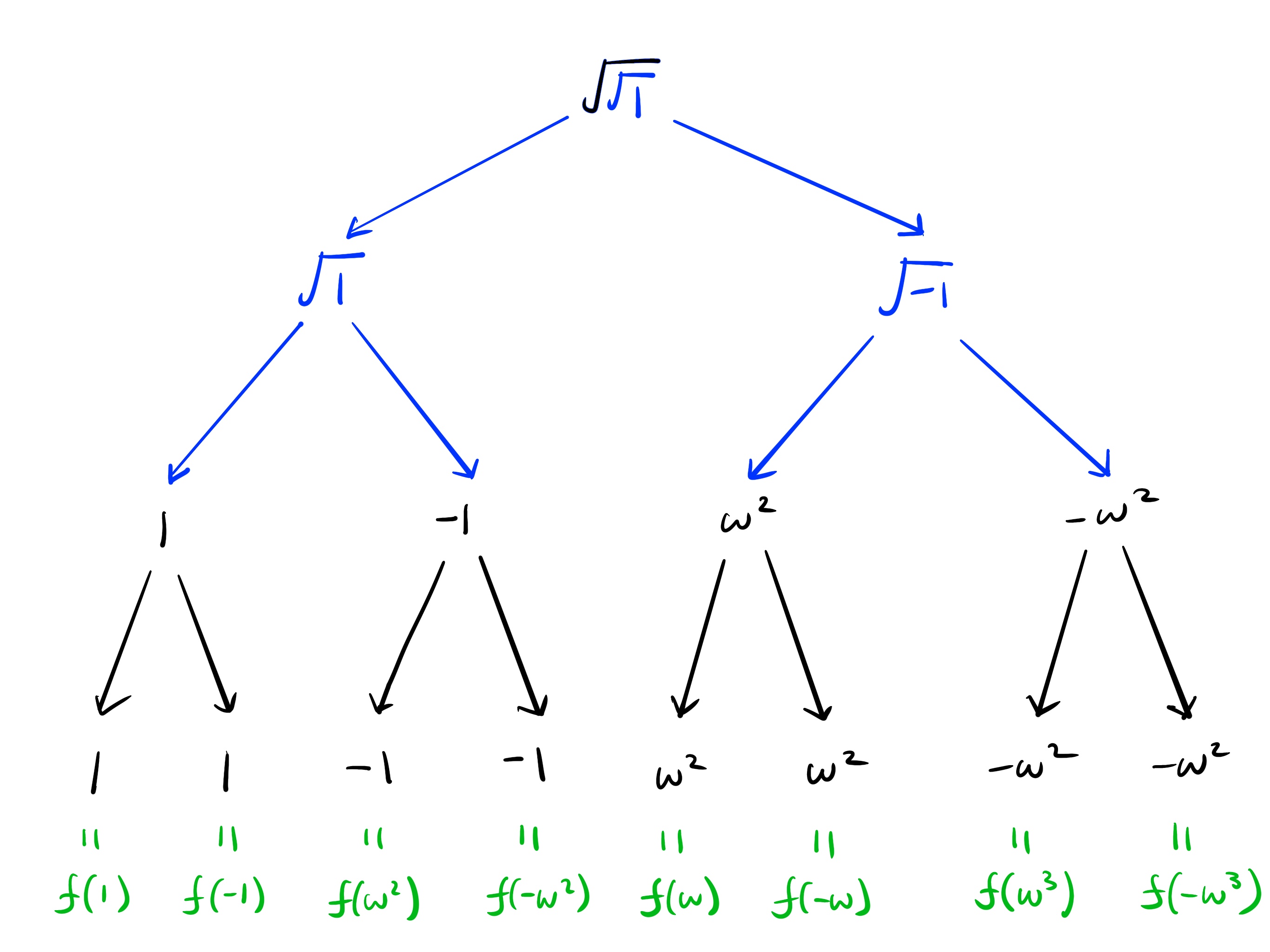
现在观察一下,如果我们直接在 上计算 1 的 8 次方根 会发生什么——结果完全相同。
在 8-th 根上计算
同样,我们将 替换为 ,这给了我们 。由于我们只有一个平方根,我们将只展开一次平方根,然后简单地复制结果下来。
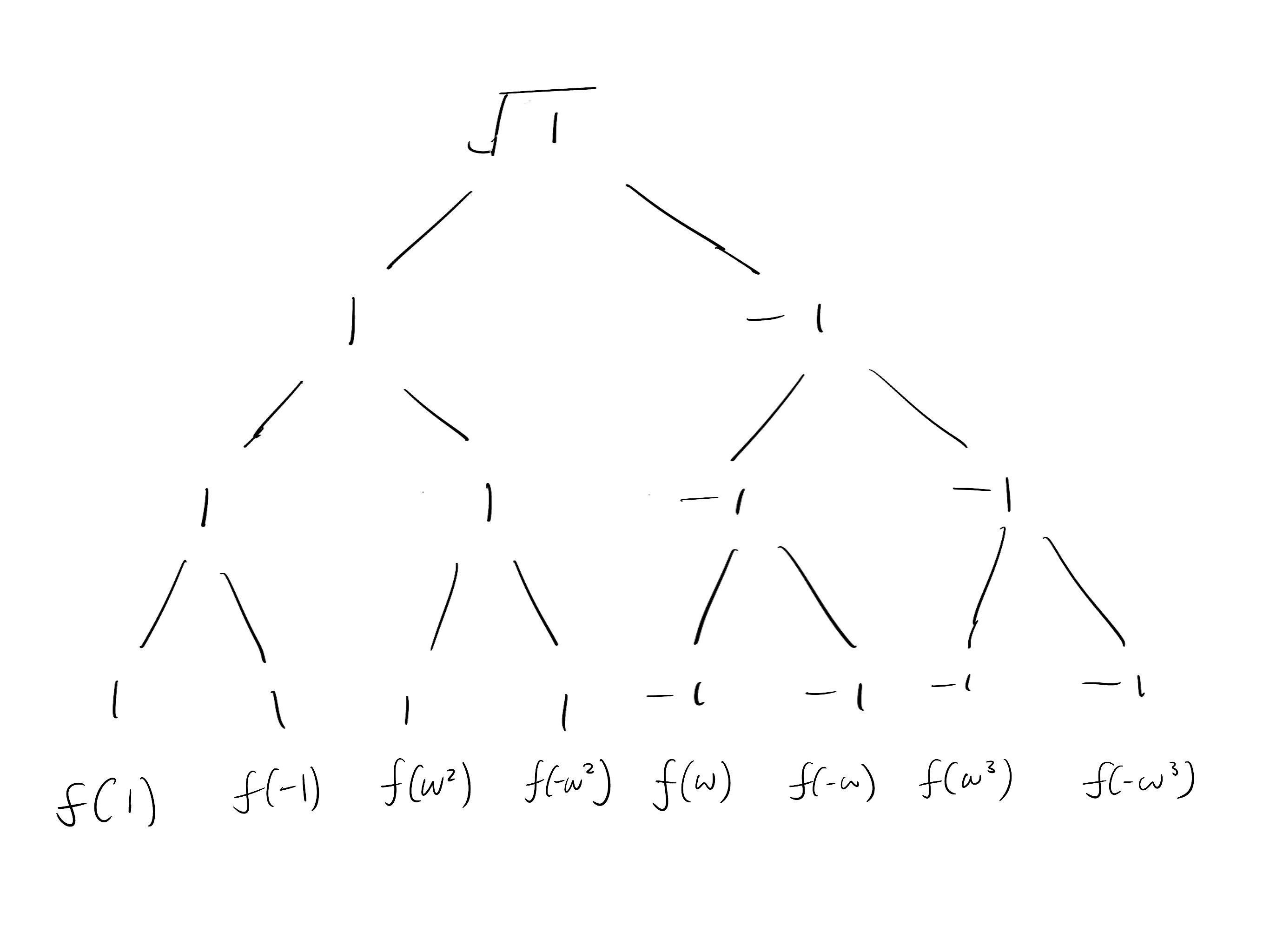
我们在之前的章节中看到,如果在 的偶数次幂上计算, 则为 1,否则为 -1。这里的结果与预期结果相符。
在 1 的 8-th 根上计算
如果我们将 替换为 ,我们会得到一个稍微尴尬的结果:
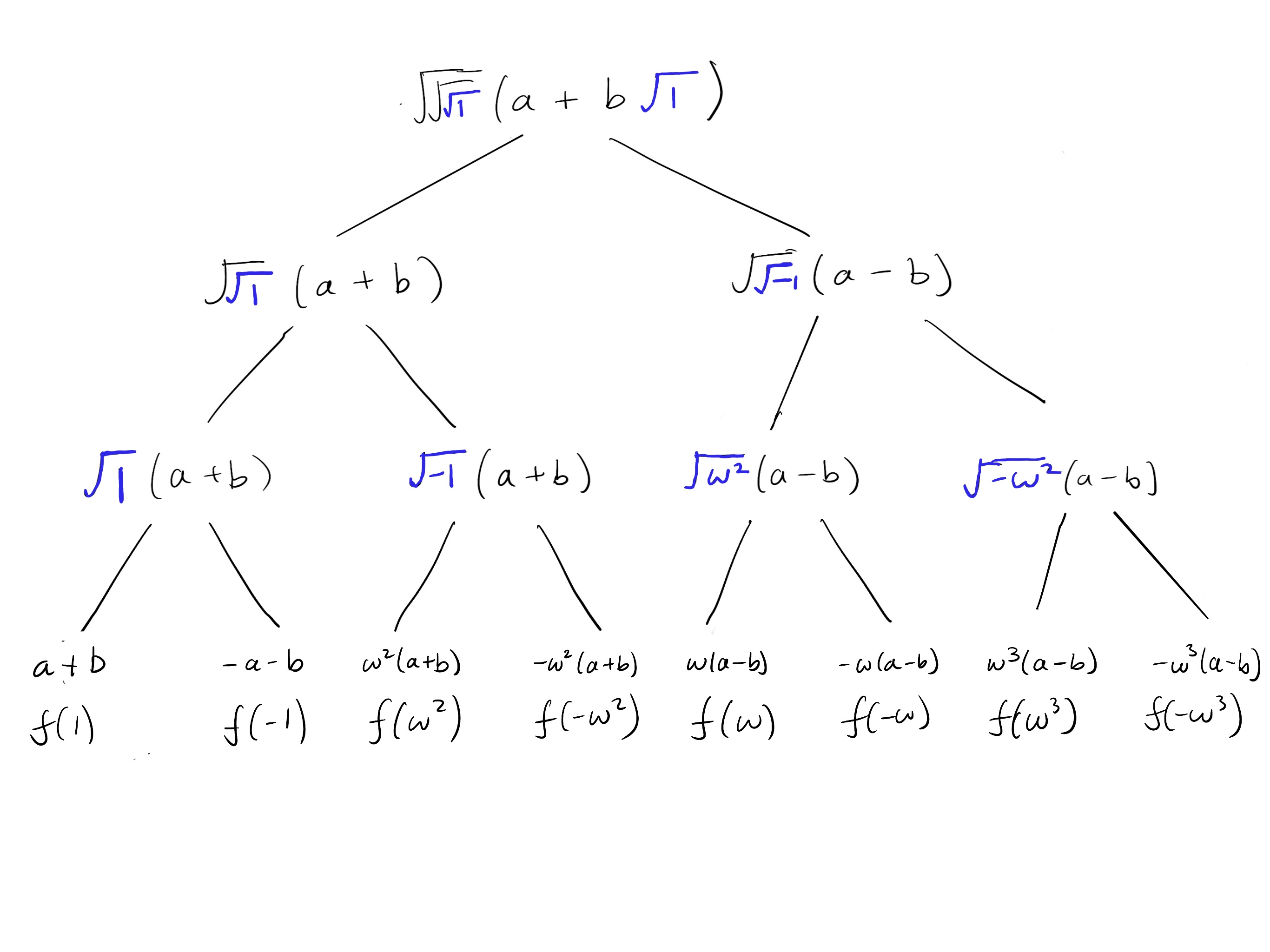
然而,如果我们首先分解 将 转换为 ,当我们将 替换为 时,新形式会变得更容易管理:
第一个平方根将在第一次计算后消失,并且 在树的大部分时间里将变为常数。
下面是一个展开平方根的图。在每个级别,我们展开(计算)一个平方根。蓝色中的平方根表示在每个步骤中计算的平方根。作为一般规则,如果平方根是嵌套的,则计算最里面的平方根:
现在让我们将结果与逐个在 1 的 8-th 根上计算 进行比较:
使用上述方法计算这些项需要 8 次加法和 16 次乘法。
但是,使用平方根展开,我们只需要 2 次加法和 10 次乘法。每当平方根展开为其两个解时,我们将其乘以相邻项。因此,每当“最终”平方根被展开时,它会导致两次乘法。这些在下面以红色高亮显示。加法以蓝色高亮显示。
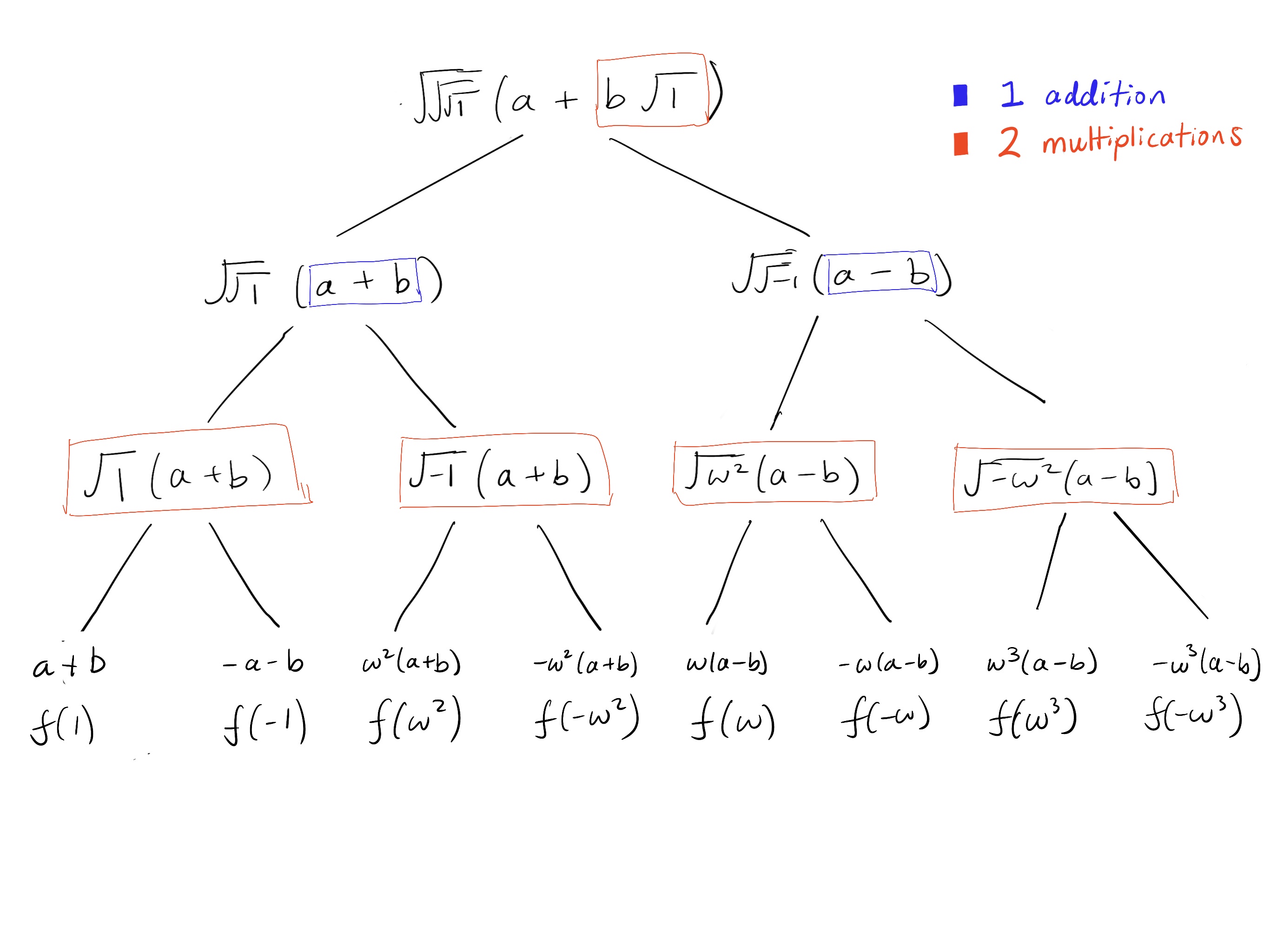
请注意,“计算平方根”是完全确定性的。我们知道它总是遵循 ,单位的 2 次方根,单位的 4 次方根,单位的 8 次方根等等的模式。因此,没有必要显式计算平方根。
简单项和困难项
我们可以看到项 最容易计算,因为它们只需要 1 次计算,其余的只是将值复制到树上。
另一方面,没有幂的 是“最难”计算的,因为我们需要在树的每一步都进行平方根展开。
函数 的好处在于,它在 函数 的 n-th 个单位根上变为多值函数 ,我们完全在树的第二层计算平方根,然后简单地复制 的总和以用于剩余的计算。
事实上,任何多项式都可以写成“最大化” 的数量,并“最小化” 的数量。
假设我们有一个 7 次多项式,我们想在 1 的 8-th 个单位根上计算它。
为了最大化 的数量并且只有一个 项,我们将其分解如下:
练习: 应该如何分解在 4th 单位根上计算的多项式 ,才能只有一个 项和尽可能多的 项?记住,在这种情况下, 是 。
在下一章中,我们将展示如何使用平方根展开来计算一般的 4 次和 8 次多项式,这恰好也是 NTT 算法。
- 原文链接: rareskills.io/post/squar...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- FFT友好的有限域 989 浏览
- 单位根的可视化表示 2244 浏览
- 单位根的平方根 2146 浏览
- k次单位根的平方是k/2次单位根 2088 浏览
- 多值函数的图像保持定理 2080 浏览
- 单位根的 k/2 次幂等于 1 或 -1 2077 浏览
- 手动实现数论变换算法 2058 浏览
- 有限域中的单位根 1979 浏览
- 点值形式下的多项式乘法 1905 浏览
- 多项式乘法 1831 浏览
- 一个密文,多个消息:FHE中的SIMD操作 2168 浏览

