点值形式下的多项式乘法

本文深入探讨了多项式乘法的优化方法，首先回顾了传统的多项式乘法，然后研究了多项式的不同表示形式（系数形式和点值形式），接着比较了在这些形式下的多项式算术，最后讨论了如何利用这些形式加速多项式乘法，并引出了数论变换（NTT）算法。文章详细解释了系数形式和点值形式之间的转换，并分析了优化转换过程以实现更快多项式乘法的策略。

多项式乘法广泛应用于零知识证明和数学密码学。但是，多项式乘法的暴力或传统方法的时间复杂度为 O(n2)，对于小输入来说还可以，但随着多项式次数的增加，成本会变得非常高。本文将详细探讨多项式乘法，以寻找使其更快的方法。

  • 我们首先回顾一下教科书/传统多项式运算
  • 接着研究多项式的不同表示形式
  • 我们检查并比较这些不同形式的多项式运算
  • 最后，我们研究这些形式如何潜在地加速多项式乘法——以及它们如何构成一种称为 数论变换 (NTT) 的算法的基础

多项式乘法 - 传统方法

考虑两个次数均为 n 的多项式 p1(x) 和 p2(x)：

p1(x)=a0+a1x+a2x2+⋯+anxnp2(x)=b0+b1x+b2x2+⋯+bnxn

使用简单的乘法对加法的分配律来乘这两个多项式的时间复杂度为 O(n2)。这里，p1(x) 的每一项都与 p2(x) 的每一项相乘：

p1(x)⋅p2(x)=p1(x)⋅(b0+b1x+⋯+bnxn)=(a0+a1x+⋯+anxn)⋅(b0+b1x+⋯+bnxn)=a0⋅(b0+b1x+⋯+bnxn)+a1x⋅(b0+b1x+⋯+bnxn)⋮+anxn⋅(b0+b1x+⋯+bnxn)

例如， 设 p1(x)=1+2x, 且 p2(x)=3+4x。

那么，

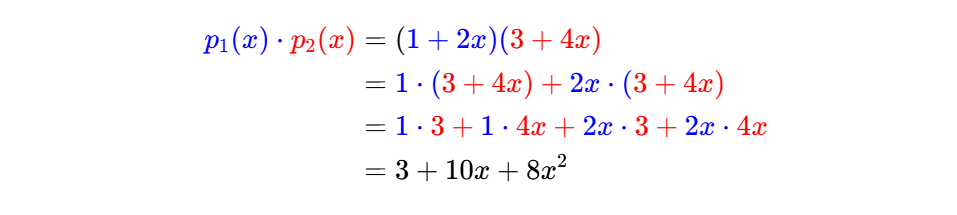
通过乘法对加法的分配律逐步计算 p1(x) 和 p2(x) 的乘积。

在编程时，这以嵌套循环的形式实现。

## 设 A 为表示 p1(x) 系数的数组
A = [a0, a1, ..., an]
## 设 B 为表示 p2(x) 系数的数组
B = [b0, b1, ..., bn]
## 设 C 为存储 p1(x).p2(x) 系数的数组

function multiply_polynomials(A, B):
    n = len(A)
    m = len(B)
    C = array of zeros of length (n + m - 1)

    for i from 0 to n - 1:
        for j from 0 to m - 1:
            C[i + j] += A[i] * B[j]
    return C

你会得到如下结果：

×34x134x2x6x8x2

对于外层循环的每次 n 次迭代，内层循环执行 n 次（假设度数相等 m=n），因此得到 n 乘以 n，即时间复杂度为 O(n2)。

我们现在想看看是否可以优化它并做得更好。或者简单地说，有没有一种方法可以使多项式乘法更快？

表示多项式的方法

我们可以用两种方式表示多项式：系数形式和点形式。

系数形式

多项式通常以所谓的单项式基表示，或者称为系数形式，这意味着它被写成变量幂的线性组合。

例如，一个 n 次多项式，当表示成

p(x)=a0+a1x+a2x2+⋯+anxn

时，是以单项式基表示的，因为它使用 [1,x,x2,…,xn] 作为其系数 a0,a1,a2,..,ax 的基。

在这种表示中，p(x) 的系数可以写成向量或数组，如 [a0,a1,…,an]，其中第一个元素对应于常数项或 x0 的系数，而最后一个元素对应于 xn 的系数。

你应该注意到，我们之前看到的分配律乘法方法（时间复杂度 O(n2) ）是在多项式的系数形式上应用的。

点（或值）形式

点（或值）形式表示是基于这样一个事实：每个 n 次多项式都可以用一组位于其上的 n+1 个不同的点来表示。

例如，考虑一个二次多项式（2 次）：

2x2−3x+1

现在取位于该曲线上的任意 3 个点（因为 n=2），例如 (0,1)、(1,0) 和 (2,3)。我们可以说这 3 个点代表给定的多项式。或者，如果我们只给出这些点，就可以从这些信息中恢复多项式 2x2−3x+1 。为什么会这样？或者我们如何能够用 n+1 个点等价地表示一个 n 次多项式？

这是因为：

对于每组 n+1 个不同的点，都存在一个唯一的最低次数多项式，其次数最多为 n，并且通过所有这些点。

这个最低次数的多项式被称为 拉格朗日多项式。

例如， 给定两个点 (1,2) 和 (3,4)，存在一个唯一的 1 次多项式（一条直线）通过这些点：

p(x)=1+x

类似地， 给定三个点 (0,1)、(1,4) 和 (2,9)，通过这些点的 2 次拉格朗日多项式是：

p(x)=1+2x+x21+2(0)+(0)2=11+2(1)+(1)2=41+2(2)+(2)2=9

给定一组点如何计算这个特殊的多项式，将在拉格朗日插值这篇文章中讨论。

拉格朗日多项式的唯一性

你必须注意，对于一组点，存在多个给定次数的多项式通过所有这些点。但只有最低次数的多项式是唯一的。

例如，在上面 (1,2) 和 (3,4) 的例子中，存在许多通过这两个点的多项式： x2−3x+4 和 2x2−7x+7 是通过这两个点的许多 2 次多项式（二次多项式）中的两个。

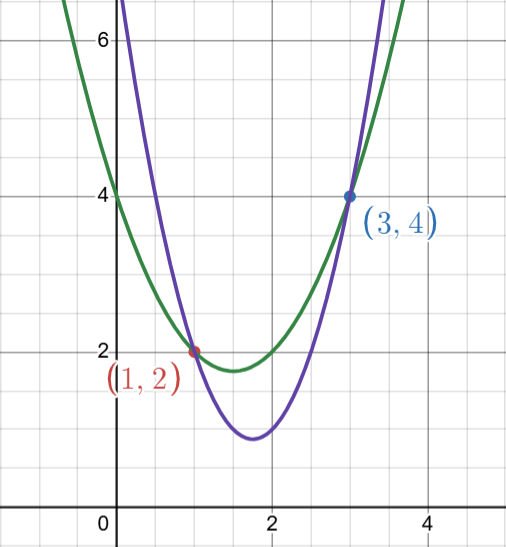
$x^2 -3x +4$ 和 $2x^2 -7x +7$，通过 $(1, 2)$ 和 $(3, 4)$ 的多个二次多项式中的两个。

类似地，如果你考虑 3 次多项式，通过点 (1,2) 和 (3,4) 的两个例子多项式是 x3−5x2+8x−2 和 −x3+4x2−2x+1。

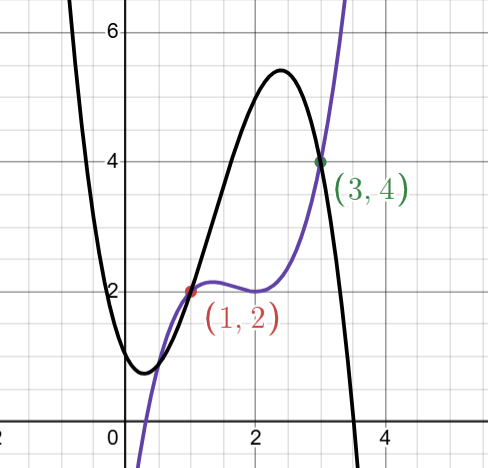
$x^3-5x^2+8x-2$ 和 $-x^3 +4x^2-2x+1$，通过 $(1, 2)$ 和 $(3, 4)$ 的两个三次多项式。

但对于最低次数，这里是 1，只存在一个最低次数的多项式，那就是 p(x)=1+x。它是唯一的，没有其他 1 次多项式可以通过这两个给定的点。

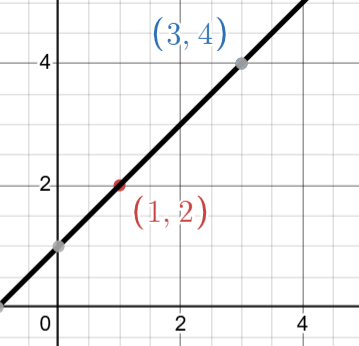
通过 $(1,2)$ 和 $(3,4)$ 的唯一线性多项式 $1+x$。

如何确定这个最低次数？

对于每组 n+1 个不同的点，存在一个唯一的次数最多为 n 的多项式通过它们。如果某些点共线或位于较低次数的多项式上，则唯一多项式的次数小于 n。因此，我们使用术语“最多 n”来涵盖次数正好为 n 的情况，以及次数较低的情况。

例如， 给定点 (1,2),(2,4) 和 (3,6)，通过它们的最低次数多项式是 y=2x。这是因为这些点共线，即它们位于一条直线上。可以检查它们之间任意两点的斜率是否相同：

4−22−1=6−43−2=2

因此，最低次数为 1，且 y=2x 是唯一的拉格朗日多项式。

类似地， 给定五个点 (−2,1),(−1,0),(0,1),(1,4),(2,9)，我们发现所有这些点都位于一个抛物线上，其方程为

y=x2+2x+1

这是一个所有给定点都位于较低次数多项式上的情况，这里是 2 次，因此拉格朗日多项式的次数为 2，小于 n（这里，n=4）。

有关最低次数多项式唯一性的证明，请参阅末尾的附录。

系数形式和点形式之间的转换

由于系数形式和点形式是等价的，我们可以很容易地在它们之间进行转换，我们现在展示一下。

插值（点形式 → 系数形式）

从点形式到系数形式的转换称为插值，是计算通过所有给定点的最低次数的多项式。最著名的方法之一是使用我们之前提到的 拉格朗日插值。如果你不熟悉它，可以阅读这篇文章。

简而言之，给定一组 (n+1) 个不同的点

{(x0,y0),(x1,y1),…,(xn,yn)}

我们可以使用拉格朗日插值公式找到唯一的最低次数多项式 p(x)，其次数最多为 n，使得：

p(xi)=yifor all i=0,1,…,n

你应该记住，拉格朗日插值的时间复杂度为 O(n2)。

求值（系数形式 → 点形式）

从系数形式到点形式的转换称为求值，是在 x 的值处对多项式进行求值，以获得相应的 y 值，从而获得一组 (xi,yi) 点，这些点表示该多项式。一种常见的做法是使用 霍纳法则（将在以后的文章中详细讨论）。

简而言之，给定多项式 p(x) 的系数 [a0,a1,…,an] 和一个值 xi，霍纳方法按如下方式计算 p(xi)：

p(xi)=a0+xi(a1+xi(a2+⋯+xian)…)

此方法一次提取 x 的公因子，直到处理完所有项。让我们看一个例子来更好地理解它。

给定多项式 p(x)=2+3x+5x2+x3 和一个值 x=2，我们将回顾霍纳法则如何计算 p(2)。

我们可以如下重写 p(x)（如上面的广义表达式所示）：

p(x)=2+x(3+x(5+x(1)))

代入 x=2：

使用霍纳方法进行逐步乘法，交替进行乘法和加法运算。

观察这些步骤如何涉及交替的乘法和加法。上述计算的步骤 1、3 和 5 是乘法，而步骤 2、4 和 6 是加法。总共有 n 次乘法和 n 次加法（这里 n=3），总时间复杂度为 O(n)。这就是霍纳法则如何在 O(n) 时间内计算给定 x 值的 n 次多项式。

因此，在 n+1 个不同的 x 值处对多项式进行求值——使用该规则从系数形式转换为点形式——需要 n 乘以 n+1，即 O(n2)。

系数形式 VS 点形式

我们说过多项式的系数形式和点形式是等价的，并且可以相互转换。也就是说，以任一形式进行加法和乘法，最终结果没有区别。让我们检查一下，首先以加法为例。

以系数形式相加

考虑两个以系数形式给出的多项式，

p1(x)=1+2x+3x2p2(x)=4+0x+1x2

或它们各自的系数数组：

p1:[1,2,3]p2:[4,0,1]

现在，将这两个多项式相加就是简单地将这两个数组按元素相加，得到的系数数组表示最终的多项式。让我们验证一下：

psum(x)=(1+4)+(2+0)x+(3+1)x2=5+2x+4x2

或者简单来说，[(1+4),(2+0),(3+1)]=[5,2,4]

对于两个 n 次多项式，我们执行 n+1 次加法来获得和的表示。因此，以系数形式进行加法的时间复杂度为 O(n)。

以点形式相加

考虑相同的两个多项式，

p1(x)=1+2x+3x2p2(x)=4+0x+1x2

首先，我们需要将它们从系数形式转换为点形式。由于这两个多项式的次数都是 2，因此它们的和的次数最多也是 2。因此，我们需要三个点来表示和（次数加 1：n+1），这需要分别对 p1(x) 和 p2(x) 进行 3 次求值。

让我们在 x=0,1,2 处计算 p1(x) 和 p2(x) 以获得我们的点。

注意：我们只是为了简单起见而选择 x=0,1,2 。你可以选择其他任意 3 个点进行求值。

  • p1(0)=1,p1(1)=6,p1(2)=17
  • p2(0)=4,p2(1)=5,p2(2)=8

现在，将这两个多项式相加需要按元素相加相应的计算结果，也就是：

  • psum(0)=(1+4)=5
  • psum(1)=(6+5)=11
  • psum(2)=(17+8)=25

这三个点 (0,5),(1,11) 和 (2,25) 给我们提供了和的点表示。让我们验证一下它们是否满足我们之前计算的多项式：

psum(x)=5+2x+4x2

  • psum(0)=5
  • psum(1)=5+2+4=11
  • psum(2)=5+4+16=25

因此，你可以看到以两种形式相加都给出了相同的结果，或者相同的多项式，只是以不同的方式表示。

在点形式加法中，对于两个 n 次多项式，有 n+1 个点表示它们中的每一个，因此我们执行 n+1 次按元素加法来获得和的代表点。因此，以点形式进行加法的时间复杂度为 O(n)。

现在，让我们也仔细看看乘法。

以系数形式相乘

考虑两个以系数形式给出的多项式：

p1(x)=1+2xp2(x)=3+4x

或它们各自的系数数组： p1=[1,2] 和 p2=[3,4]

使用之前讨论的分配律方法进行乘法运算：

pprod(x)=(1)(3+4x)+(2x)(3+4x)=3+4x+6x+8x2=3+10x+8x2

结果多项式为 pprod(x)=3+10x+8x2，用系数数组 [3,10,8] 表示。正如我们在本文开头所看到的，系数形式乘法的分配律方法的时间复杂度为 O(n2)。

以点形式相乘

我们现在考虑相同的多项式并将它们转换为点形式。

p1(x)=1+2xp2(x)=3+4x

由于两个多项式的次数均为 1，因此它们的乘积的次数最多为 2，这意味着我们需要 3 个点来表示它，这需要分别对 p1(x) 和 p2(x) 进行 3 次求值。

因此，让我们在 x=0,1,2 处计算 p1(x) 和 p2(x)。

  • p1(0)=1,p1(1)=3,p1(2)=5
  • p2(0)=3,p2(1)=7,p2(2)=11

现在，要获得表示其乘积的点，我们按元素相乘计算结果：

  • pprod(0)=1⋅3=3
  • pprod(1)=3⋅7=21
  • pprod(2)=5⋅11=55

因此，三个点 (0,3),(1,21) 和 (2,55) 给我们提供了结果乘积的点表示。

让我们验证一下它们是否满足我们之前得到的乘积多项式：

pprod(x)=3+10x+8x2

  • pprod(0)=3
  • pprod(1)=3+10+8=21
  • pprod(2)=3+20+32=55

因此，你可以看到以两种形式相乘都给出了相同的多项式，只是以不同的方式表示。

总之，对于两个 n 次多项式 p1(x) 和 p2(x)，它们的乘积的次数最多为 2n，这意味着我们需要 2n+1 个点来表示它。因此，我们在 x 的公共值处对每个多项式执行 2n+1 次求值，以将它们转换为点形式：

p1(x0),p1(x1),p1(x2),…p1(x2n)p2(x0),p2(x1),p2(x2),…p2(x2n)

然后，我们通过按元素相乘这两个集合来进行点形式乘法，这需要 2n+1 次乘法，即时间复杂度为 O(n)。

p1(x0)⋅p2(x0),p1(x1)⋅p2(x1),…,p1(x2n)⋅p2(x2n)

这给了我们 2n+1 个点，这些点表示乘积 p1(x).p2(x)：

{(x0,p1(x0)⋅p2(x0)),(x1,p1(x1)⋅p2(x1)),…,(x2n,p1(x2n)⋅p2(x2n))}

这里需要注意的惊人之处在于，系数形式和点形式的加法都需要相同的时间 O(n)，而点形式的乘法比系数形式快得多。在点形式中，我们执行 2n+1 次按元素乘法，时间复杂度为 O(n)，这比系数形式乘法所需的 O(n2) 好得多！

但是，仍然存在一个问题——我们没有考虑转换为点形式和反之亦然的开销。

因此，让我们看一下点形式乘法的完整过程，其中包括三个步骤：

  1. 将系数形式转换为点形式 我们对两个要相乘的 n 次多项式在 (2n+1) 个 x 值处进行求值，以获得每个多项式的 (2n+1) 个计算结果的集合。使用霍纳方法，这需要 O(n2)。
  2. 点形式表示中的按元素乘法 我们按元素相乘这两个集合，以获得 (2n+1) 个计算结果，这些结果给出了其乘积的点形式表示。这需要 O(n)。
  3. 将点形式转换为系数形式 我们计算通过所有结果 (2n+1) 个点的唯一最低次数多项式（系数形式）。使用拉格朗日插值，这需要 O(n2)。

因此，上述步骤的总体时间复杂度为：

O(n2)+O(n)+O(n2)≈O(n2)

这并不比我们开始时的情况更好。因此，我们需要探索是否有任何优化可以使此过程更快。

优化转换

要记住的关键点是，系数形式的乘法需要 O(n2)，而点形式的乘法（按元素）需要 O(n)。因此，如果我们能找到一种比 O(n2) 更快的方法来将系数形式转换为点形式，反之亦然（上述步骤 1 和 3），我们可以优化乘法以在亚二次时间内运行。

重要的是要注意，我们无法优化多项式加法，因为系数形式和点形式的加法都以 O(n) 运行。

所以现在让我们集思广益，想想如何更快地从系数形式转换为点形式。

如果我们知道一个点的求值可以给我们几个相关点的值，从而节省我们重复计算，那会怎么样？

例如，如果我们有一个具有对称图的多项式，则计算一个点将告诉我们其相应对称点的计算结果。

考虑多项式 p(x)=x2。 观察一下，

p(−2)=4andp(2)=4

一个 $x^2$ 的图像，显示了 $x=-2$ 和 $x=2$ 的对称值。

或者，更简单地说，观察如何对于所有 xi，

p(−xi)=p(xi)

这不仅适用于 p(x)=x2，而且推广到所有仅包含偶数次幂系数的多项式，这些多项式也称为偶多项式。

例如，考虑偶多项式（仅包含 x 的偶数次幂项：

q(x)=x10+3x8−2x6+3x4−2x2−x0

一个 $x^{10}+3x^{8}-2x^{6}+3x^{4}-2x^{2}-x^{0}$ 的图像，显示了关于 y 轴的对称曲线。

在上图中，很容易观察到

q(x)=q(−x)

从视觉上看，偶多项式的图是关于 y 轴镜像的，并且对于任何给定 x 的正值和负值，它们的值都相同。

那么仅包含奇数次幂系数的奇多项式怎么样呢？ 考虑 p(x)=x3。 观察一下

p(−2)=−8=−p(2)

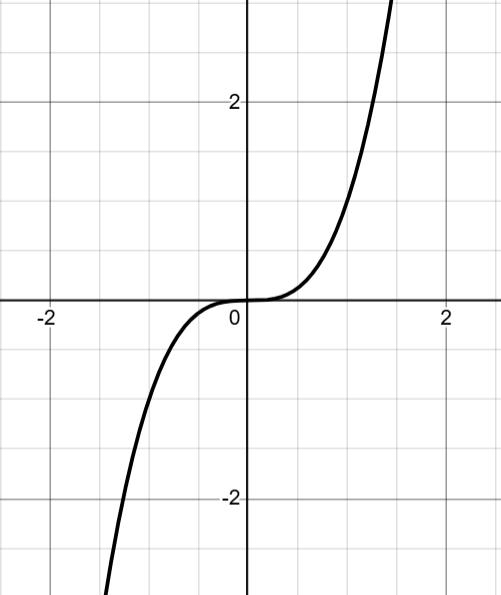
一个 $x^3$ 的图像，显示了关于原点的对称性。

在上图中，观察如何对于所有 xi，

p(−xi)=−p(xi)

同样，这不仅适用于 p(x)=x3，而且推广到所有奇多项式，即仅包含 x 的奇数次幂项的多项式。例如，考虑多项式

q(x)=−x7+3x5+x3−x

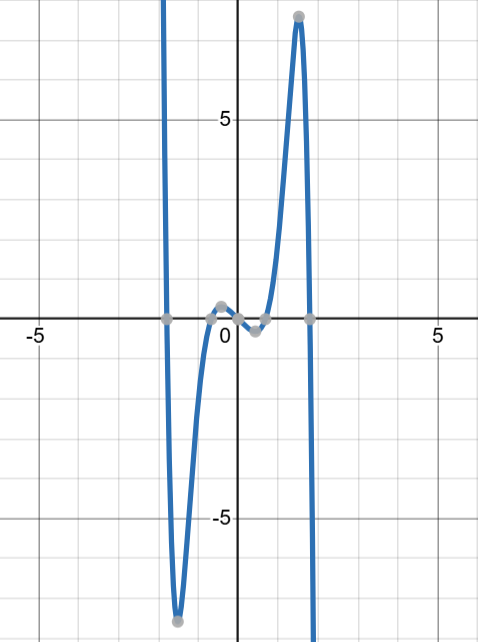
一个 $x^{7}+3x^{5}+x^{3}-x$ 的图像，显示了关于原点的对称性。

在上图中，观察到

q(x)=−q(−x)

从视觉上看，所有奇多项式的图都关于原点对称，这使得上述等式对它们都成立。

现在你可以看到，在计算了某些点之后，我们可以在没有任何额外计算的情况下获得其他点的计算结果。例如，在上面的示例中，对于偶多项式和奇多项式，知道 p(x) 的计算结果也给了我们 p(−x) 的计算结果。

我们可以利用这一事实来加快多项式乘法，这正是一个叫做 数论变换 (NTT) 的漂亮算法允许我们做的。NTT 通过递归地使用某些点的对称性属性，使求值和插值的时间复杂度为 O(nlog⁡n)，从而使转换变为亚二次。

但是由于 NTT 在有限域上运行，因此我们无法使用 x 的负值。这就是乘法子群、循环性和单位根的概念发挥作用的地方。这些概念将使我们能够利用有限域中存在的对称性来更有效地执行多项式乘法。我们将在以后的文章中详细探讨 NTT 的工作原理。

附录

最低次数多项式唯一性证明

我们证明，如果存在两个次数相等的 polynomials p(x) 和 q(x) 插值一组点，那么必须存在一个 polynomial r(x) 使得 r(x)=p(x)−q(x)。

然后我们将证明 r(x) 的唯一可能解是 r(x)=0，否则我们将得到一个比其次数具有更多根的多项式，我们证明这是不可能的。现在让我们详细看一下这些步骤。

让我们假设最低次数的拉格朗日多项式不是唯一的。 那么至少存在两个不同的最低次数多项式，通过所有给定的 n+1 个点。设这两个多项式为 p(x) 和 q(x)。现在，将 polynomial r(x) 定义为 p(x) 和 q(x) 之间的差。

r(x)=p(x)–q(x)

现在，如果我们证明对于 x 的所有值，r(x) 都为 0，那么我们将证明 p(x) 等于 q(x)，因此拉格朗日多项式是唯一的。

由于 p(x) 和 q(x) 的次数都最多为 n，因此从简单的代数减法可知，r(x) 的次数也必须最多为 n。 此外，由于 p(x) 和 q(x) 都通过相同的 n+1 个点，因此对于每个 x 值，它们的值都相同。

注意： 如图所示，当两个不同的多项式对于给定的 x 值具有相同的 y 值时，表示它们在该点相交。例如：

p(x)=x2和q(x)=2x。

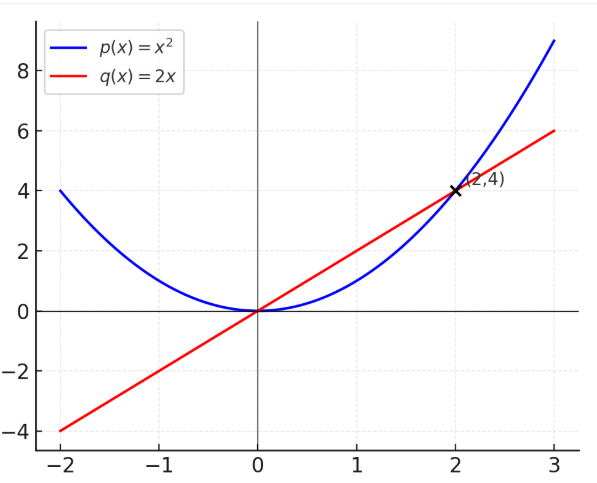
一个图像，显示 $x^2$ 和 $2x$ 如何在 $(0,0)$ 和 $(2,4)$ 相交。

在 x=2 处，两者都给出 y=4 ，因此它们在点 (2,4) 相交。 在本例中，我们处理的是不同的多项式。对于给定的 x 具有相同的 y 值的另一种可能是它们实际上是相同的多项式！在这种情况下，对于 x 的所有值，它们都将具有相同的 y 值，而不仅仅是对于 x 的某些特定值。

对于 p(x) 和 q(x)，对于至少 n + 1 个不同的 x 值，它们的值都相同。这可以用数学方式表示为：

p(xi)=q(xi)∀i∈{0,1,…,n}

因此，p(x) 和 q(x) 在所有 n+1 个点处的差将为零。也就是说，

r(xi)=p(xi)−q(xi)=0∀i∈{0,1,…,n}

因此，r(x) 在 n+1 个点处的值为零，这意味着它是一个零多项式。让我们更清楚地了解原因。

零多项式是指对于 x 的所有值，其值都为零的多项式。零多项式的最简单示例是：

p(x)=0

另一种看待它的方式是，如果我们的多项式求值域——可以在这里计算多项式的点的集合——比如 S={x0,x1⋯,xn−1}，那么该域的零多项式可以是：

p(x)=(x−x0)(x−x1)⋯(x−xn−1)

因为，

p(x)=0∀x∈{x0,x1,⋯xn−1}

我们可以有更多的域 S 的零多项式，例如：

f1(x)=p(x)f2(x)=p(x)2f3(x)=0⋅p(x)

请注意，f1(x)、f2(x) 和 f3(x) 中的每一个在域 S 上计算都为零，因此是一个零多项式。我们可以有更多。最原始的是 f3(x)=0，即常数零本身。

注意：如果将域 S 视为所有实数的集合，那么我们唯一可以拥有的零多项式是 f(x)=0 ，因为没有其他多项式对于所有实数都计算为零。

现在观察我们看到的每个示例零多项式的根数和次数。

多项式的根是域中多项式计算为零的值，而多项式的次数是你熟知的变量的最高幂。

  • f1(x)：根数- n，次数- n
  • f2(x)：根数- n，次数- 2n
  • f3(x)：根数- n，次数- 0

所有这些在 S 上计算都为零；因此，根数为 n，而次数可以通过修改 p(x) 来改变，p(x) 的次数为 n。

另请注意，f3(x)=0 的根数大于其次数。这只有在零多项式的情况下才有可能，特别是原始多项式 f3(x)=0。否则，根数始终小于或等于次数。

考虑一个非零的 n 次多项式；它最多可以有 n 个根（或与 x 轴的交点）。原始零多项式是唯一的例外，因为它的根数大于其次数。

例如， 一个 2 次二次方程，例如 q(x)=x2−3x+2，有两个根，即 x=1 和 x=2。

一个向上开口的抛物线 $x^2-3x+2$，在点 $x = 1$ 和 $x = 2$ 与 x 轴相交的图像。

对于一个二次方程要具有大于两个根，它必须等于零，即 q(x)=0。

现在，回到我们的论点：由于 r(x) 在 n+1 个点处的值为零，它必须至少具有 n+1 个根，这大于其次数 n。因此 r(x) 必须等于零。

p(x)−q(x)=r(x)=0

这意味着 p(x)=q(x)，意味着它们是相同的多项式。因此，插值一组 n+1 个不同点的最低次数多项式是唯一的。

  • 原文链接： rareskills.io/post/polyn...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
RareSkills
RareSkills
https://www.rareskills.io/

RareSkills

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！