使用多项式的纠删码

当查克·诺里斯使用纠删码时，他不仅仅是保护数据的冗余性；他创造了一个坚不可摧的冗余堡垒，即使丢失一个字节都感觉像是在向他道歉。

使用多项式插值的纠删码

定义

纠删码是一种前向纠错（FEC）码，它基于比特擦除（而不是比特错误）的假设，将 k 个符号的消息转换为更长的消息（码字），包含 n 个符号，这样原始消息可以从 n 个符号的子集中恢复。

我们现在将看到一个使用多项式的纠删码例子。

警告

本节缺乏许多数学形式，并隐藏了许多关于实际实现的细节（比如我们实际上会在有限域上的多项式上操作，而本节在实数上的多项式上操作）。

然而，本节让读者掌握了使用多项式插值的纠删码的思想。

问题设置

Alice有以下4字节的消息 0x160C0B0D，她想发送给Bob。为此，她使用了一个不可靠的网络（互联网），连接非常糟糕，非常容易丢失数据。

Alice会将消息编码成一个6字节的编码消息，如果Bob只收到编码后的6字节消息的任何75%，他都能够重构出原始的4字节消息。

任何这个词在这里非常重要。Bob必须能够重构原始数据，如果他收到例如：

• 只有编码消息的前75%，或者
• 只有编码消息的最后75%，或者
• 任何组合，只要Bob收到了至少75%（6字节）的编码消息

注意

在本节中，我们将使用3/4（75%）的代码率，这意味着初始消息大小将增加50%。因此，只需要编码消息的3/4（75%）就可以重构初始消息。

编码

让我们将Alice的4字节消息分成4个字节：[0x16, 0x0C, 0x0B, 0x0D]。

每个字节将代表一个多项式约束。我们有4个约束。

让我们定义一个多项式 P，它具有以下约束：

• P(0) = 22 ( 0x16)
• P(1) = 12 ( 0x0C)
• P(2) = 11 ( 0x0B)
• P(3) = 13 ( 0x0D)

x 的取值是整数 (0, 1, 2, 3)。

P(x) 的取值是Alice想要编码的消息的字节。

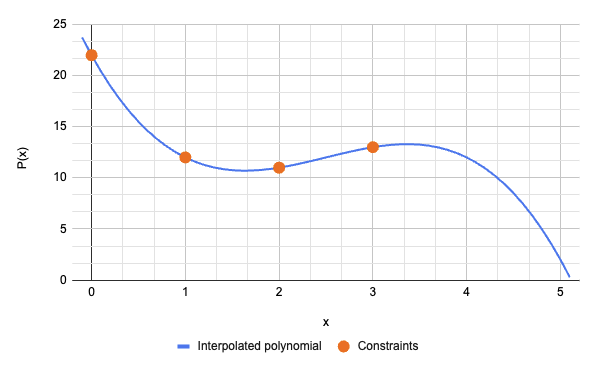
使用拉格朗日多项式插值，Alice找到了唯一的次数最多为 4-1 = 3 的多项式，它符合这4个约束。她得到：

\[\ P(x) =-x^3 + \frac{15}{2}x^2 - \frac{33}{2}x + 22\ \]

扩展

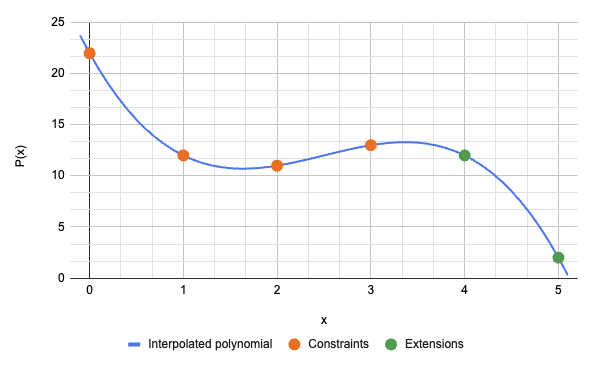
Alice添加了2个扩展点。她选择了对应于 x=3 和 x=4 的2个点。

在这些点上评估 P 得到：

• P(4) = 12 ( 0x0C)
• P(5) = 2 ( 0x02)

通信

Alice不会将 0x160C0B0D 发送给Bob，而是：

• 与Bob约定她将向他发送6个 (x, P(x)) 数据点，其中 P 是一个次数最多为 3 的多项式。
• 向Bob发送：[(0x00, 0x16), (0x01, 0x0C), (0x02, 0x0B), (0x03, 0x0D), (0x04, 0x0C), (0x05, 0x02)]，对应于 6 个 (x, P(x)) 元组。
• 与Bob约定初始数据是：[P(0), P(1), P(2), P(3)]。

由于Alice和Bob之间的连接容易丢失数据，Bob只收到了6个元组中的4个：

• (0x00, 0x16),
• (0x02, 0x0B),
• (0x04, 0x0C), 和
• (0x05, 0x02)

重构

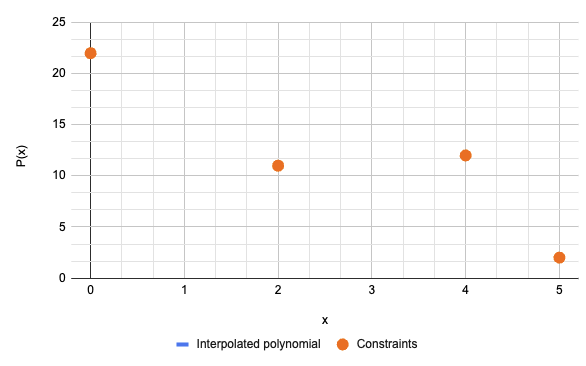
从收到的字节中，Bob推断出：

• P(0) = 22 ( 0x16)
• P(2) = 11 ( 0x0B)
• P(4) = 12 ( 0x0C)
• P(5) = 2 ( 0x02)

Bob知道原始消息是 [P(0), P(1), P(2), P(3)]。

然而，P(1) 和 P(3) 丢失了。

Bob知道这4个点属于次数最多为 3 的唯一多项式，所以他可以使用拉格朗日插值法重构多项式（就像Alice之前做的那样，但是使用对应于4字节初始消息的 4 个点）。

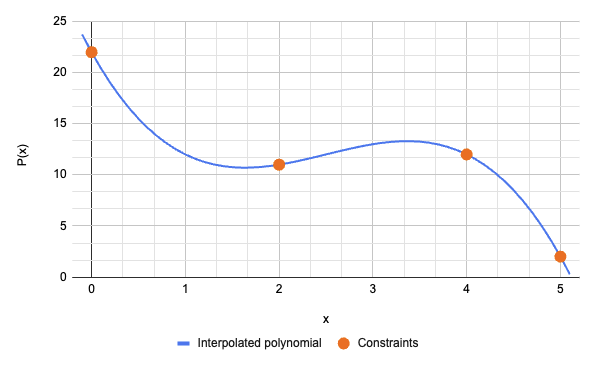
Bob最终得到这个多项式（这与Alice之前计算的完全相同）：

\[\ P(x) =-x^3 + \frac{15}{2}x^2 - \frac{33}{2}x + 22\ \]

Bob现在评估 P 在 x=1 和 x=3 处的值。

他发现：

• P(1) = 12 ( 0x0C)
• P(3) = 13 ( 0x0D)

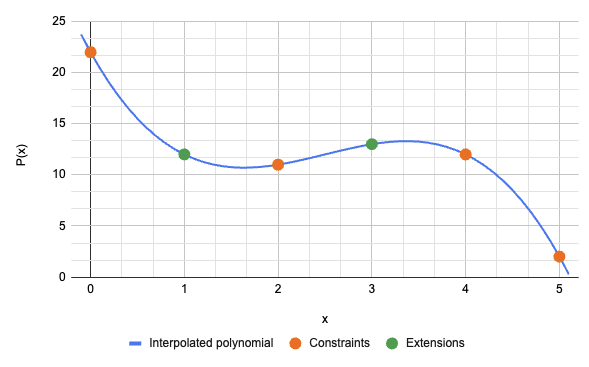
Bob现在能够重构前4个元组：[(0x00, 0x16), (0x01, 0x0C), (0x02, 0x0B), (0x03, 0x0D)] 和初始消息：0x160C0B0D。

注意

如果Bob收到的点少于4个，那么他将无法重构次数最多为 3 的对应唯一多项式。

实际上，他将能够重构无穷多个次数最多为 3 的多项式，包括原始多项式。

但是，他不会确切地知道哪个才是好的那个。

注意

使用这种纠删码技术的优势可能在第一眼并不明显：

• 在没有纠删码的情况下，Alice向Bob发送4个字节的数据。
• 在使用纠删码的情况下，Alice向Bob发送6个字节的数据（+ x 坐标）。

纠删码消耗更多数据。

然而，这里的重要一点是：

• 在没有纠删码的情况下，Bob必须收到Alice发送的正好4个字节中的4个（100%）。
• 在使用纠删码的情况下，Bob可能只收到Alice发送的6个字节中的任何4个（75%）。

一些纠删码的实际应用

二维码

此二维码嵌入了 offchainlabs.com 链接。

如果我们损坏此二维码的某些部分，仍然可以检索嵌入在其中的（纠删码）信息。

光盘

一张刮伤损坏的光盘（在一定程度上......）可能仍然可以读取，因为存储在其中的数据是经过纠删码的。

以太坊 - 信标链 blob peer DAS

这个具体的案例将被详细研究。

• 原文链接： hackmd.io/@manunalepa/ry...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～